2.3.1 Grandeza
Grandeza é tudo aquilo que se pode pesar, medir e contar. De acordo com Bellemain e Lima (2002) a Grandeza também pode ser vista como uma propriedade dos objetos; o aspecto de sua conservação, isto é, o fato de que mesmo que o objeto mude de posição ou de forma, algo pode permanecer constante, que pode ser usado como critério para ordenar uma coleção de objetos.
Segundo o Instituto de Pesos e Medidas do Estado de São Paulo (2021), ainda, “Grandeza pode ser definida, resumidamente, como sendo o atributo físico de um corpo que pode ser qualitativamente distinguido e quantitativamente determinado”.
Em Bellemain e Lima (2002, p. 43), as Grandezas são vistas como classes de equivalência, como por exemplo, as classes de equivalência de superfícies que têm a mesma área. Eles explicam:
De um ponto de vista estritamente matemático, a relação de equivalência “ter mesma área” (que permite considerar a área enquanto grandeza), é definida pela escolha de uma unidade seguida da medida das superfícies: duas superfícies de mesma medida têm mesma área.
O conceito de Grandeza atribui significado a outros conceitos matemáticos como os de número, pois “o conjunto numérico adequado para a construção da medida de uma grandeza deve ser o conjunto dos reais, face ao conhecido fenômeno da existência de quantidades incomensuráveis” (BELLEMAIN; LIMA, 2002, p. 100). Ou seja, no caso das Grandezas geométricas, estas relacionam a geometria, a álgebra e os sistemas numéricos.
As Grandezas são classificadas em dois tipos: as discretas e as contínuas. Lima (1991a, p. 7) as diferencia e exemplifica:
[…] as discretas (como um rebanho) e as contínuas (como o tempo, o peso e a distância). Comparar uma grandeza discreta com a unidade significa efetuar uma contagem; o resultado é sempre um número inteiro. Se, entretanto, a grandeza é contínua, compará-la com a unidade é medi-la; o resultado da comparação (medida) é um número real. Se a grandeza contínua que se quer medir é comensurável com a unidade escolhida, a medida é um número racional; se é incomensurável, sua medida é um número irracional.
Uma estrutura axiomática para o conceito de Grandeza foi feita por Bellemain e Lima (2002, p. 99-117), apresentaremos ela a seguir.
Para estruturar esse modelo matemático os autores inicialmente consideraram as Grandezas escalares e admitiram a Teoria dos Conjuntos, as regras lógicas e o conjunto dos naturais 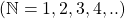 , com sua estrutura de semigrupo aditivo ordenado e comutativo. Além disso, o modelo axiomático apresentado por eles tomou o conjunto dos racionais estritamente positivos para valores das medidas.
, com sua estrutura de semigrupo aditivo ordenado e comutativo. Além disso, o modelo axiomático apresentado por eles tomou o conjunto dos racionais estritamente positivos para valores das medidas.
Para construir o conceito mais geral de Grandeza de maneira formal, os autores buscaram tornar logicamente precisa a expressão “o atributo  de elementos de um conjunto”. E, para isso, o caminho seguido por eles foi definir uma relação de equivalência entre dois elementos de um conjunto e, em seguida, considerar o conjunto das classes induzido por essa relação, isto é, cada uma delas passando a ser “o atributo
de elementos de um conjunto”. E, para isso, o caminho seguido por eles foi definir uma relação de equivalência entre dois elementos de um conjunto e, em seguida, considerar o conjunto das classes induzido por essa relação, isto é, cada uma delas passando a ser “o atributo  ”. Por exemplo, para definir o comprimento de um segmento de reta, num dado universo
”. Por exemplo, para definir o comprimento de um segmento de reta, num dado universo 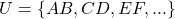 de segmentos de reta, recorre-se a relação de equivalência “ter o mesmo comprimento”, a ser verificada entre dois segmentos de reta, e então, forma-se o conjunto
de segmentos de reta, recorre-se a relação de equivalência “ter o mesmo comprimento”, a ser verificada entre dois segmentos de reta, e então, forma-se o conjunto 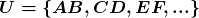 das classes de equivalência de
das classes de equivalência de 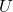 com respeito a essa relação de equivalência, e cada uma dessas classes,
com respeito a essa relação de equivalência, e cada uma dessas classes, 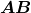 , passa a ser, então, o comprimento de
, passa a ser, então, o comprimento de 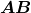 .
.
O procedimento adotado pelos autores para uma Grandeza arbitrária 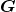 iniciou por tomar um conjunto
iniciou por tomar um conjunto 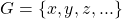 . Então, definiu-se uma relação de equivalência entre os elementos de
. Então, definiu-se uma relação de equivalência entre os elementos de  . Ou seja, uma relação que satisfaça, para quaisquer elementos
. Ou seja, uma relação que satisfaça, para quaisquer elementos  ,
, 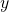 e
e  de
de  , as seguintes condições:
, as seguintes condições:
Axioma 1. 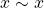 (reflexividade);
(reflexividade);
Se 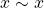 diz-se que “
diz-se que “ e
e 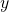 são equivalentes com respeito à Grandeza
são equivalentes com respeito à Grandeza  ”. Na interpretação do exemplo dos segmentos de reta, tem-se: “
”. Na interpretação do exemplo dos segmentos de reta, tem-se: “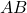 e
e 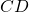 são equivalentes com respeito ao comprimento” ou simplesmente “
são equivalentes com respeito ao comprimento” ou simplesmente “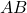 e
e 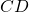 têm o mesmo comprimento” (BELLEMAIN; LIMA, 2002).
têm o mesmo comprimento” (BELLEMAIN; LIMA, 2002).
Axioma 2. 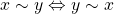 (simetria);
(simetria);
Axioma 3. 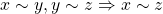 (transitividade).
(transitividade).
Em seguida, os autores admitiram a existência de uma relação em  simbolizada por
simbolizada por 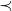 , tal que, para dois elementos quaisquer
, tal que, para dois elementos quaisquer  e
e 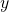 pertencentes a
pertencentes a  , ocorre uma e só uma das situações:
, ocorre uma e só uma das situações:
Axioma 4. 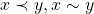 ou
ou 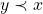 (tricotomia).
(tricotomia).
Se 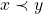 diz-se “
diz-se “ é menor do que
é menor do que 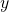 ”. No caso dos segmentos de reta
”. No caso dos segmentos de reta 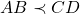 deve-se ler “
deve-se ler “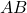 tem comprimento menor do que
tem comprimento menor do que 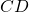 ”. A transitividade dessa relação é também suposta (BELLEMAIN; LIMA, 2002):
”. A transitividade dessa relação é também suposta (BELLEMAIN; LIMA, 2002):
Axioma 5. 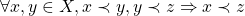 .
.
Utilizando os axiomas de 1 a 5, os autores deduziram duas proposições, válidas para quaisquer 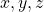 no conjunto
no conjunto  :
:
Proposição 1. 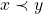 e
e 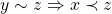 .
.
Proposição 2. 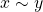 e
e 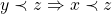 .
.
Neste ponto, os autores ressaltaram o fato de que toda relação de equivalência num conjunto  permite definir o conjunto das classes de equivalência que são constituídas tomando-se, para cada elemento
permite definir o conjunto das classes de equivalência que são constituídas tomando-se, para cada elemento  em
em  , a classe
, a classe 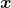 de todos os elementos equivalentes a
de todos os elementos equivalentes a  . Forma-se, então, o conjunto
. Forma-se, então, o conjunto 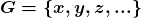 , denominado um “domínio de quantidades de Grandeza
, denominado um “domínio de quantidades de Grandeza  “. Os elementos
“. Os elementos 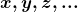 de
de  são “quantidades da Grandeza
são “quantidades da Grandeza  “, ou, nos casos em que a Grandeza
“, ou, nos casos em que a Grandeza  é subentendida, simplesmente “quantidades”. Também, chamam-se os elementos
é subentendida, simplesmente “quantidades”. Também, chamam-se os elementos 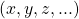 de
de  de “valores da Grandeza
de “valores da Grandeza  “, ou apenas Grandezas. No mais, quando se está lidando com mais de uma Grandeza, a expressão “domínio de quantidades da Grandeza
“, ou apenas Grandezas. No mais, quando se está lidando com mais de uma Grandeza, a expressão “domínio de quantidades da Grandeza  ” é, em geral, simplificada para “Grandeza
” é, em geral, simplificada para “Grandeza  ”, ou mesmo, “
”, ou mesmo, “ ”.
”.
Pelo Axioma 4, todos os elementos do conjunto  passam a ser comparáveis, obtendo-se uma relação de ordem total. Assim, os autores transportaram para o conjunto
passam a ser comparáveis, obtendo-se uma relação de ordem total. Assim, os autores transportaram para o conjunto  , das classes de equivalência, essa relação de ordem definida no conjunto base
, das classes de equivalência, essa relação de ordem definida no conjunto base  . Para duas classes quaisquer
. Para duas classes quaisquer 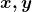 pertencentes a
pertencentes a  , definiram
, definiram
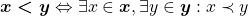 .
.
As Proposições 1 e 2 garantem que a definição acima não depende dos representantes  e
e 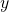 escolhidos nas respectivas classes
escolhidos nas respectivas classes 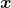 e
e 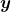 , assegurando que a relação de ordem acima está bem definida. Além disso, a igualdade
, assegurando que a relação de ordem acima está bem definida. Além disso, a igualdade 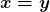 , sendo uma igualdade entre dois conjuntos, significa que todo elemento de
, sendo uma igualdade entre dois conjuntos, significa que todo elemento de 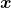 pertence a
pertence a 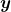 e, reciprocamente, todo elemento de
e, reciprocamente, todo elemento de 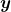 pertence a
pertence a 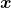 . Dessa maneira, para
. Dessa maneira, para 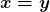 , se
, se  e
e 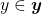 , então
, então 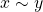 (BELLEMAIN; LIMA, 2002).
(BELLEMAIN; LIMA, 2002).
Os axiomas e propriedades que regem as relações  e
e 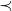 foram traduzidas pelos autores em proposições relativas ao conjunto
foram traduzidas pelos autores em proposições relativas ao conjunto  das classes e podem ser demonstradas sem dificuldades (BELLEMAIN; LIMA, 2002).
das classes e podem ser demonstradas sem dificuldades (BELLEMAIN; LIMA, 2002).
Proposição 3. A relação  no conjunto
no conjunto  é uma relação de equivalência, ou seja, é uma relação reflexiva, simétrica e transitiva.
é uma relação de equivalência, ou seja, é uma relação reflexiva, simétrica e transitiva.
Proposição 4. Para quaisquer 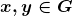 , verifica-se uma e só uma das alternativas:
, verifica-se uma e só uma das alternativas: 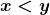 ;
; 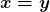 ;
; 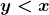 .
.
Proposição 5. Para quaisquer 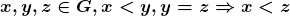 .
.
Proposição 6. Para quaisquer 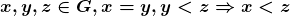 .
.
Resulta das propriedades enunciadas que a relação 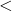 é uma relação de ordem estrita no conjunto
é uma relação de ordem estrita no conjunto  , pois, em virtude da Proposição 4, dois elementos quaisquer de
, pois, em virtude da Proposição 4, dois elementos quaisquer de  são sempre comparáveis (BELLEMAIN; LIMA, 2002).
são sempre comparáveis (BELLEMAIN; LIMA, 2002).
Assim, destacaram os autores, as Grandezas que satisfazem as propriedades formalizadas acima podem ser chamadas Grandezas ordinais e é possível aritmetizar tais Grandezas, isto é, estabelecer uma função que associe a cada quantidade um número. Mas, para essa correspondência, é necessário que haja isomorfismo entre as estruturas de ordem nas grandezas nos números reais, ou seja, se uma quantidade é menor do que outra o número associado a primeira deve ser menor do que o da segunda.
Os autores destacaram que o maior interesse da exposição feita residiu nas Grandezas que, além de ordinais, admitem uma operação de adição entre as suas quantidades. Essas Grandezas, ordinais e aditivas, são chamadas “Grandezas mensuráveis”. No que se segue, os autores procuraram axiomatizar uma operação de adição que modelize, por exemplo, a operação de colocar um segmento de reta com a origem coincidindo com a extremidade de outro, alinhados, para produzir uma combinação de dois segmentos.
Assim, iniciaram por introduzir axiomaticamente uma adição em  , definindo-a, no entanto, apenas para elementos
, definindo-a, no entanto, apenas para elementos 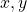 que sejam distintos. Esta última restrição reflete a impossibilidade física de se efetuar a combinação dita anteriormente com apenas um segmento de reta (BELLEMAIN; LIMA, 2002):
que sejam distintos. Esta última restrição reflete a impossibilidade física de se efetuar a combinação dita anteriormente com apenas um segmento de reta (BELLEMAIN; LIMA, 2002):
Axioma 6. Para dois elementos distintos quaisquer de  define-se um elemento de
define-se um elemento de  , simbolizado por
, simbolizado por 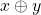 , que satisfaz as seguintes condições para qualquer
, que satisfaz as seguintes condições para qualquer 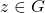 , desde que as adições estejam definidas:
, desde que as adições estejam definidas:
i) 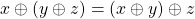 (associatividade);
(associatividade);
ii) 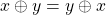 (comutatividade);
(comutatividade);
iii) 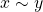 e
e 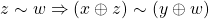 ;
;
iv) 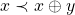 ;
;
v) 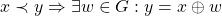 .
.
Os autores, utilizando o procedimento padrão, transportaram para o conjunto  das classes de equivalência de
das classes de equivalência de  relativamente à relação
relativamente à relação  , definindo uma operação binária em
, definindo uma operação binária em  , por meio dos representantes das classes de
, por meio dos representantes das classes de  . Para contornar a dificuldade na definição de
. Para contornar a dificuldade na definição de 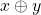 , em que é necessário supor
, em que é necessário supor 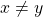 , e, além do mais, possibilitar a adição de um número qualquer de parcelas, os autores introduziram outro axioma:
, e, além do mais, possibilitar a adição de um número qualquer de parcelas, os autores introduziram outro axioma:
Axioma 7. Para cada 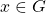 , existe um número infinito de elementos
, existe um número infinito de elementos 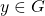 , tais que
, tais que 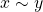 e
e 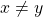 .
.
Esse axioma equivale ao requisito de que as classes de  possuem um número infinito de elementos. Com base no que eles admitiram anteriormente, é possível, então, definir a operação binária desejada (BELLEMAIN; LIMA, 2002):
possuem um número infinito de elementos. Com base no que eles admitiram anteriormente, é possível, então, definir a operação binária desejada (BELLEMAIN; LIMA, 2002):
Definição 1. Sejam 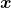 e
e 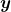 elementos de
elementos de  . Tomem-se
. Tomem-se  e
e 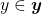 , efetue-se a adição
, efetue-se a adição 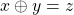 e considere-se a classe
e considere-se a classe 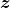 do elemento
do elemento  . Por definição,
. Por definição, 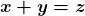 .
.
Primeiro, foi destacado pelos autores que é possível efetuar a operação 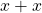 , pois o Axioma 7 permite a escolha de representantes distintos na classe
, pois o Axioma 7 permite a escolha de representantes distintos na classe 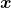 . Em seguida, foi notado que é possível transportar as propriedades da adição válidas para o conjunto base
. Em seguida, foi notado que é possível transportar as propriedades da adição válidas para o conjunto base  , para o conjunto das classes
, para o conjunto das classes  , enunciado no que se segue.
, enunciado no que se segue.
Proposição 7. Para quaisquer 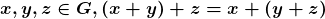 .
.
Proposição 8. Para quaisquer 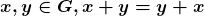 .
.
Proposição 9. Para quaisquer 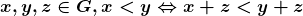 .
.
Proposição 10. Para quaisquer 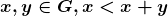 .
.
Proposição 11. Para quaisquer 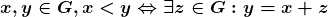 .
.
Proposição 12. Para quaisquer 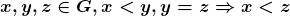 .
.
Proposição 13. Para quaisquer 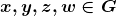 ,
,
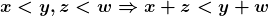 .
.
Completada a axiomatização da adição de quantidades de uma Grandeza, os autores passaram a considerar uma multiplicação de uma quantidade por um número 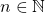 . A ideia é considerar uma operação do conjunto
. A ideia é considerar uma operação do conjunto 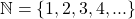 sobre o conjunto
sobre o conjunto  (BELLEMAIN; LIMA, 2002).
(BELLEMAIN; LIMA, 2002).
Dado um natural 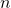 e um elemento
e um elemento 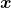 de
de  definem
definem 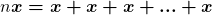 (
(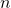 vezes).
vezes).
Mais rigorosamente, definem tal operação usando a regra de recorrência:
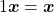
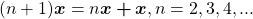
Nessa definição, sendo o operador a multiplicação, a primeira linha diz que 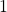 multiplicado pela classe
multiplicado pela classe 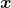 é igual a própria classe
é igual a própria classe 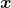 . Na segunda linha dessa definição, usando recorrência, temos à esquerda da igualdade (utilizando o leitor como referência)
. Na segunda linha dessa definição, usando recorrência, temos à esquerda da igualdade (utilizando o leitor como referência) 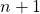 multiplicado pela classe
multiplicado pela classe 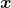 , que é igual a
, que é igual a 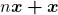 , à direita da igualdade. Note que os dois sinais de adição que aparecem nessa igualdade têm naturezas distintas e estão em mundos diferentes. No lado esquerdo, esse sinal de adição
, à direita da igualdade. Note que os dois sinais de adição que aparecem nessa igualdade têm naturezas distintas e estão em mundos diferentes. No lado esquerdo, esse sinal de adição 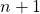 é a adição que aprendemos ao estudarmos os Axiomas de Peano, está relacionada a ideia de sucessor. Já o sinal de adição do lado direito da igualdade é o operador de classes da Definição 1.
é a adição que aprendemos ao estudarmos os Axiomas de Peano, está relacionada a ideia de sucessor. Já o sinal de adição do lado direito da igualdade é o operador de classes da Definição 1.
Do ponto de vista matemático, os autores definiram uma ação do monoide cujo conjunto base é o conjunto dos números naturais e cuja operação binária é o produto usual (produto usual de números reais) sobre o conjunto das classes de equivalência definidas pela relação de equivalência  , o conjunto
, o conjunto 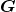 . Em outras palavras, é uma ação do monoide dos naturais com a multiplicação usual sobre o conjunto
. Em outras palavras, é uma ação do monoide dos naturais com a multiplicação usual sobre o conjunto 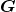 das classes de equivalência.
das classes de equivalência.
Ao utilizar essa ação os autores obtêm ganhos significativos. Um deles, é que se ganha, de imediato, uma identificação envolvendo dois sinais distintos de mundos distintos (a igualdade da segunda linha). Um segundo ganho significativo é que se tem uma distributividade tal qual como funciona na adição e multiplicação de números reais, por exemplo. Uma outra contribuição também significativa é que, em decorrência dessa identificação que os autores fizeram, das Proposições 14 à 26 se ganha um arcabouço teórico de propriedades que permitem ter uma estrutura de anel, mais especificamente para esse trabalho, um anel booleno, que é o espaço adequado onde trabalhamos Teoria da Medida.
As propriedades abaixo foram apresentadas pelos autores:
Proposição 14. Para todo 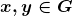 e para todo
e para todo  , são válidas as igualdades:
, são válidas as igualdades:
i) 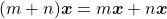 ;
;
ii) 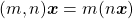 ;
;
iii) 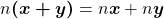 .
.
Proposição 15. Para todo 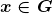 e para todo
e para todo 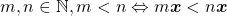 .
.
Proposição 16. Para todo 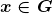 e para todo
e para todo 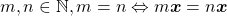 .
.
Proposição 17. Para todo 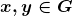 e para todo
e para todo 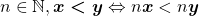 .
.
Proposição 18. Para todo 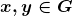 e para todo
e para todo 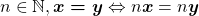 .
.
As proposições acima fornecem as regras de uma “álgebra das quantidades” (ou uma “álgebra das Grandezas”) no caso de os coeficientes serem números naturais. A etapa seguinte que os autores percorreram é a extensão dessa álgebra para os coeficientes no conjunto 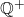 dos racionais estritamente positivos (BELLEMAIN; LIMA, 2002). Para isso, os autores introduziram a divisão de uma quantidade por um número natural e iniciaram por observar que, para cada
dos racionais estritamente positivos (BELLEMAIN; LIMA, 2002). Para isso, os autores introduziram a divisão de uma quantidade por um número natural e iniciaram por observar que, para cada 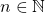 , pode ser definido um operador:
, pode ser definido um operador:
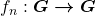
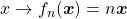
A Proposição 17 mostra que, se 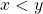 então
então 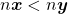 . Assim, a função
. Assim, a função 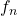 é injetiva de
é injetiva de  em
em  (BELLEMAIN; LIMA, 2002). Os autores adotaram, então, o seguinte axioma:
(BELLEMAIN; LIMA, 2002). Os autores adotaram, então, o seguinte axioma:
Axioma 8. (Divisibilidade) Dados 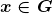 e
e 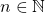 , existe
, existe 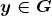 tal que
tal que 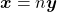 .
.
O elemento 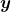 acima definido é dito a
acima definido é dito a 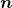 -ésima parte de
-ésima parte de 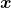 sendo simbolizado por
sendo simbolizado por 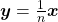 . Como a função
. Como a função 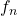 é injetiva o elemento
é injetiva o elemento 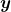 é único. Pôde-se, então, ser definido o operador
é único. Pôde-se, então, ser definido o operador 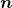 -ésima parte, a saber, a função
-ésima parte, a saber, a função 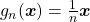 (BELLEMAIN; LIMA, 2002).
(BELLEMAIN; LIMA, 2002).
O coeficiente 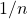 na expressão de
na expressão de 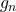 não é o número racional
não é o número racional 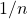 , mas apenas uma notação que caracteriza de forma conveniente o operador
, mas apenas uma notação que caracteriza de forma conveniente o operador 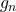 (BELLEMAIN; LIMA, 2002). A identificação deste operador com o número racional é precisamente o objetivo das etapas que se seguem da explanação dos autores. Para isso, desenvolveram regras operatórias com os coeficientes
(BELLEMAIN; LIMA, 2002). A identificação deste operador com o número racional é precisamente o objetivo das etapas que se seguem da explanação dos autores. Para isso, desenvolveram regras operatórias com os coeficientes 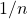 que imitam aquelas já obtidas para os coeficientes naturais. Foi preciso, no entanto, que os autores contornassem nesta etapa expressões do tipo
que imitam aquelas já obtidas para os coeficientes naturais. Foi preciso, no entanto, que os autores contornassem nesta etapa expressões do tipo 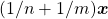 ou do tipo
ou do tipo ![Rendered by QuickLaTeX.com [(1/m)(1/n)] \boldsymbol{x}](http://blogs.multimeios.ufc.br/fernandacarmo/wp-content/ql-cache/quicklatex.com-b6f47d2d4ae1a07d689d9291f0458024_l3.png) , pois ainda não seria possível atribuir significado a tais expressões.
, pois ainda não seria possível atribuir significado a tais expressões.
As primeiras propriedades que serão mencionadas resultaram diretamente da definição do operador 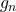 :
:
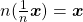 ,
,
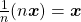 .
.
Outras propriedades se seguiram e são demonstradas pelos autores:
Proposição 19. Para todo 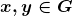 e para todo
e para todo  , tem-se:
, tem-se:
i) ![Rendered by QuickLaTeX.com \frac{1}{m} \boldsymbol{x}+ \frac{1}{n} \boldsymbol{x}= \frac{1}{mn}[(m+n) \boldsymbol{x}]](http://blogs.multimeios.ufc.br/fernandacarmo/wp-content/ql-cache/quicklatex.com-9a90f5132ec6eea41a048bf20e80f911_l3.png) ;
;
ii) 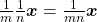 ;
;
iii) 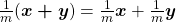 .
.
Demonstração da primeira igualdade:
i) ![Rendered by QuickLaTeX.com mn[\frac{1}{m} \boldsymbol{x}+ \frac{1}{n} \boldsymbol{x}]=mn(\frac{1}{m} \boldsymbol{x})+mn(\frac{1}{n} \boldsymbol{x})=n[m(\frac{1}{m} \boldsymbol{x})]+m[n(\frac{1}{n} \boldsymbol{x})]=](http://blogs.multimeios.ufc.br/fernandacarmo/wp-content/ql-cache/quicklatex.com-782073b0723510604bd63d8668eab4bc_l3.png)
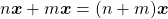 .
.
Proposição 20. Para todo 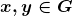 e para todo
e para todo 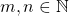 , tem-se:
, tem-se:
i) 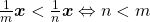 ,
,
ii) 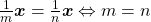 ,
,
iii) 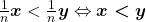 ,
,
iv) 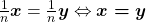 .
.
Demonstração da primeira parte da proposição:
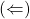 Suponha-se que
Suponha-se que 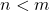 . Se não se tem
. Se não se tem 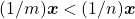 , dever-se-á ter
, dever-se-á ter 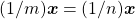 ou
ou 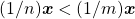 . No primeiro caso, virá
. No primeiro caso, virá 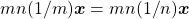 , donde resulta
, donde resulta  e, portanto,
e, portanto,  , contrariando a hipótese. No segundo caso, deduz-se que
, contrariando a hipótese. No segundo caso, deduz-se que 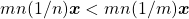 , que implica na desigualdade
, que implica na desigualdade 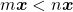 e, portanto,
e, portanto,  , o que contradiz a hipótese (BELLEMAIN; LIMA, 2002).
, o que contradiz a hipótese (BELLEMAIN; LIMA, 2002).
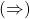 Seja
Seja 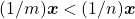 . Suponha, por absurdo, que não ocorre
. Suponha, por absurdo, que não ocorre 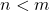 . Deverá, então ser
. Deverá, então ser  ou
ou  . No primeiro caso tem-se, de imediato,
. No primeiro caso tem-se, de imediato, 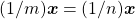 , contradizendo a hipótese. Na segunda alternativa, levando em conta a proposição direta resulta
, contradizendo a hipótese. Na segunda alternativa, levando em conta a proposição direta resulta 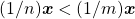 , contrariamente à hipótese. Logo,
, contrariamente à hipótese. Logo, 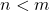 , como se queria provar (BELLEMAIN; LIMA, 2002).
, como se queria provar (BELLEMAIN; LIMA, 2002).
Neste ponto, os autores trataram de compor dois operadores 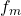 e
e 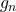 sendo
sendo  . Uma propriedade útil para essa definição foi dada na:
. Uma propriedade útil para essa definição foi dada na:
Proposição 21. Para todo 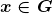 e para todo
e para todo  , tem-se
, tem-se 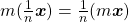 .
.
Definiu-se, então,
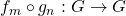
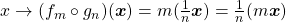 .
.
O operador acima foi representado por 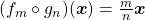 .
.
Novamente, neste ponto, os autores advertiram que o coeficiente da Grandeza na definição acima não representa um número racional e sim uma notação para o operador composto de uma multiplicação por um número natural 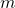 com uma divisão pelo número natural
com uma divisão pelo número natural 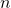 . Seguindo etapas análogas às que foram seguidas quando se tratava de
. Seguindo etapas análogas às que foram seguidas quando se tratava de 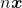 e de
e de 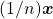 , podem ser demonstradas as proposições que se seguem.
, podem ser demonstradas as proposições que se seguem.
Proposição 22. Para todo 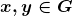 e para todo
e para todo 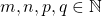 , tem-se:
, tem-se:
i) 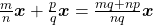 ,
,
ii) 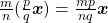 ,
,
iii) 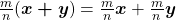 .
.
Proposição 23. Para todo 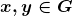 e para todo
e para todo 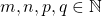 , tem-se:
, tem-se:
i) 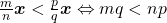 ,
,
ii) 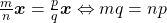 ,
,
iii) 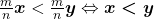 ,
,
iv) 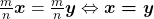 .
.
As condições sobre 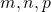 e
e 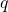 da Propriedade i) foram apresentadas da forma indicada pelo fato de que nessa exposição ainda não tinham sido atribuídos significados para relações do tipo
da Propriedade i) foram apresentadas da forma indicada pelo fato de que nessa exposição ainda não tinham sido atribuídos significados para relações do tipo 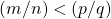 (BELLEMAIN; LIMA, 2002).
(BELLEMAIN; LIMA, 2002).
Proposição 24. Para todo 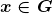 e para todo
e para todo 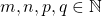 , tem-se
, tem-se 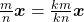 .
.
Os autores destacaram que a proposição acima permite que se possam eliminar fatores primos comuns aos números que compõem o par ordenado representado por 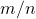 . Dado um par ordenado
. Dado um par ordenado 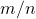 , o procedimento referido permite definir um par ordenado
, o procedimento referido permite definir um par ordenado 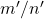 , denominado par ordenado reduzido de
, denominado par ordenado reduzido de 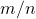 , em que
, em que 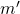 e
e 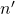 são primos entre si e
são primos entre si e 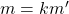 e
e 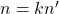 , para algum número natural
, para algum número natural 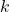 .
.
Proposição 25. Seja 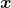 um elemento qualquer de
um elemento qualquer de  . Se
. Se 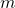 e
e 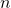 são primos entre si e se
são primos entre si e se 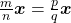 então, existe um número natural
então, existe um número natural 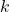 tal que
tal que 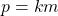 e
e 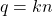 .
.
Proposição 26. Dois operadores 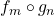 e
e 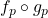 têm o mesmo efeito sobre um elemento de
têm o mesmo efeito sobre um elemento de  se, e somente se, os pares reduzidos de
se, e somente se, os pares reduzidos de 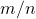 e de
e de 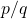 forem iguais.
forem iguais.
As proposições que foram enunciadas até aqui permitiram que se considere o conjunto dos operadores 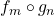 , para
, para 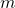 e
e 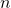 arbitrários, e que nesse conjunto se possa definir a relação de equivalência induzida pela Proposição 26. Com isso, foi possível definir um espaço
arbitrários, e que nesse conjunto se possa definir a relação de equivalência induzida pela Proposição 26. Com isso, foi possível definir um espaço 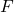 de classes de operadores sobre
de classes de operadores sobre  denominadas operadores de fracionamento ou operadores racionais (BELLEMAIN; LIMA, 2002). Os autores tomaram, então, nesse espaço, as operações de adição e decomposição de classes de operadores induzidas pelas igualdades válidas para quaisquer
denominadas operadores de fracionamento ou operadores racionais (BELLEMAIN; LIMA, 2002). Os autores tomaram, então, nesse espaço, as operações de adição e decomposição de classes de operadores induzidas pelas igualdades válidas para quaisquer 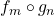 e
e 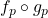 :
:
![Rendered by QuickLaTeX.com [(f_{m} \circ g_{n})+(f_{p} \circ g_{p})] (\boldsymbol{x})= \frac{m}{n} \boldsymbol{x}+ \frac{p}{q} \boldsymbol{x}= \frac{mq+np}{nq} \boldsymbol{x}](http://blogs.multimeios.ufc.br/fernandacarmo/wp-content/ql-cache/quicklatex.com-ed520c97209af878bd70c801e3c6448c_l3.png) ,
,
![Rendered by QuickLaTeX.com [(f_{m} \circ g_{n}) \circ (f_{p} \circ g_{p})] (\boldsymbol{x})= \frac{m}{n} (\frac{p}{q} \boldsymbol{x})= \frac{mp}{nq}\boldsymbol{x}](http://blogs.multimeios.ufc.br/fernandacarmo/wp-content/ql-cache/quicklatex.com-2c0936e7e713c659e4d651dd95cd079a_l3.png) .
.
É possível provar que o espaço 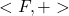 , constituído pelo conjunto
, constituído pelo conjunto 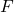 e pela operação de adição, é um semigrupo comutativo. Igualmente, é um semigrupo comutativo o espaço
e pela operação de adição, é um semigrupo comutativo. Igualmente, é um semigrupo comutativo o espaço 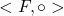 e, além disso, é válida a distributividade da operação de composição relativamente à adição (BELLEMAIN, LIMA, 2002).
e, além disso, é válida a distributividade da operação de composição relativamente à adição (BELLEMAIN, LIMA, 2002).
Os autores consideraram, então, o conjunto 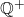 dos racionais estritamente positivos, munido das operações usuais de adição e multiplicação de racionais. Verifica-se, por meio de uma demonstração simples, que existe um isomorfismo entre as estruturas
dos racionais estritamente positivos, munido das operações usuais de adição e multiplicação de racionais. Verifica-se, por meio de uma demonstração simples, que existe um isomorfismo entre as estruturas 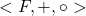 e
e 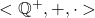 . Em outros termos, é possível provar a existência de uma identificação entre o espaço de operadores de fracionamento e os números racionais estritamente positivos.
. Em outros termos, é possível provar a existência de uma identificação entre o espaço de operadores de fracionamento e os números racionais estritamente positivos.
Por simplicidade, os autores sempre supõem que os números naturais que definem o operador 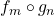 são primos entre si, ou seja, são pares ordenados reduzidos; além disso para tornar mais leve a linguagem, dizemos o “operador
são primos entre si, ou seja, são pares ordenados reduzidos; além disso para tornar mais leve a linguagem, dizemos o “operador 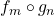 ” em vez de “a classe do operador
” em vez de “a classe do operador 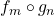 ”.
”.
Uma observação é feita pelos autores. Na construção do sistema axiomático exposto poderia ter sido considerado como conjunto dos coeficientes o conjunto dos naturais em vez do conjunto dos racionais positivos. Então, ter-se-ia uma estrutura para o conceito de Grandeza do tipo 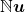 , constituída pelos múltiplos naturais de uma unidade
, constituída pelos múltiplos naturais de uma unidade 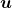 . Assim, essa estrutura inclui o próprio sistema dos números naturais, que podem ser entendidos como quantidades de uma Grandeza ou, simplesmente, como Grandezas. Desse modo, a unidade usada seria o número 1. Esse é o modelo abstrato das chamadas Grandezas discretas.
. Assim, essa estrutura inclui o próprio sistema dos números naturais, que podem ser entendidos como quantidades de uma Grandeza ou, simplesmente, como Grandezas. Desse modo, a unidade usada seria o número 1. Esse é o modelo abstrato das chamadas Grandezas discretas.
No entanto, adotando o conjunto dos números racionais para os coeficientes, como foi apresentado, vê-se, similarmente, que os racionais positivos podem ser interpretados como Grandezas. Neste caso, temos um modelo abstrato de Grandeza indefinidamente divisível que possui continuidade. De fato, apenas quando se toma, nesse tipo de sistema axiomático adotado, os números reais como o conjunto dos coeficientes do sistema, pode-se obter um modelo abstrato para as Grandezas contínuas (BELLEMAIN, LIMA, 2002).
Essa é uma axiomática construída pelos autores que considera uma Grandeza como um conjunto de objetos, ditos quantidades dessa Grandeza, no qual está definida uma relação de ordem, uma operação interna de soma de duas quantidades e uma operação externa de produto de uma quantidade por um número racional estritamente positivo. Os axiomas adotados permitiram construir uma “Grandeza”, ou um “domínio de quantidades”, como um semiespaço vetorial, 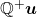 , constituído pelos múltiplos,
, constituído pelos múltiplos, 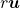 , de uma dada quantidade
, de uma dada quantidade 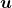 , escolhida arbitrariamente como unidade de medida.
, escolhida arbitrariamente como unidade de medida.
Além disso, de acordo com os autores, tais axiomas delimitam as regras de uma “álgebra de quantidades” na qual são válidas, por exemplo, igualdades do tipo 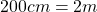 em que expressa igualdade entre duas quantidades da Grandeza comprimento, isto é, uma igualdade entre dois comprimentos. Ou seja, é uma igualdade que expressa um mesmo comprimento representado em duas unidades diferentes, no caso, o centímetro e o metro. Ou ainda,
em que expressa igualdade entre duas quantidades da Grandeza comprimento, isto é, uma igualdade entre dois comprimentos. Ou seja, é uma igualdade que expressa um mesmo comprimento representado em duas unidades diferentes, no caso, o centímetro e o metro. Ou ainda, 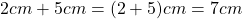 , que envolve a operação de adição de duas quantidades, um conceito primitivo (sem definição, portanto) na estrutura matemática que foi apresentada. A validade dessa cadeia de igualdades resulta das regras adotadas como axiomas no mencionado sistema lógico, bem como da definição de
, que envolve a operação de adição de duas quantidades, um conceito primitivo (sem definição, portanto) na estrutura matemática que foi apresentada. A validade dessa cadeia de igualdades resulta das regras adotadas como axiomas no mencionado sistema lógico, bem como da definição de 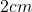 e
e 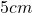 , cada um deles sendo um produto de um número racional por uma quantidade. Do ponto de vista formal, a álgebra utilizada nesse exemplo é inteiramente análoga à álgebra dos polinômios, na qual
, cada um deles sendo um produto de um número racional por uma quantidade. Do ponto de vista formal, a álgebra utilizada nesse exemplo é inteiramente análoga à álgebra dos polinômios, na qual 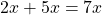 .
.

2.3 Grandezas e Medidas
|

Início
|

2.3.2 Medida
|
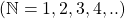 , com sua estrutura de semigrupo aditivo ordenado e comutativo. Além disso, o modelo axiomático apresentado por eles tomou o conjunto dos racionais estritamente positivos para valores das medidas.
, com sua estrutura de semigrupo aditivo ordenado e comutativo. Além disso, o modelo axiomático apresentado por eles tomou o conjunto dos racionais estritamente positivos para valores das medidas. de elementos de um conjunto”. E, para isso, o caminho seguido por eles foi definir uma relação de equivalência entre dois elementos de um conjunto e, em seguida, considerar o conjunto das classes induzido por essa relação, isto é, cada uma delas passando a ser “o atributo
de elementos de um conjunto”. E, para isso, o caminho seguido por eles foi definir uma relação de equivalência entre dois elementos de um conjunto e, em seguida, considerar o conjunto das classes induzido por essa relação, isto é, cada uma delas passando a ser “o atributo  ”. Por exemplo, para definir o comprimento de um segmento de reta, num dado universo
”. Por exemplo, para definir o comprimento de um segmento de reta, num dado universo 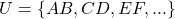 de segmentos de reta, recorre-se a relação de equivalência “ter o mesmo comprimento”, a ser verificada entre dois segmentos de reta, e então, forma-se o conjunto
de segmentos de reta, recorre-se a relação de equivalência “ter o mesmo comprimento”, a ser verificada entre dois segmentos de reta, e então, forma-se o conjunto 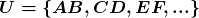 das classes de equivalência de
das classes de equivalência de 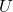 com respeito a essa relação de equivalência, e cada uma dessas classes,
com respeito a essa relação de equivalência, e cada uma dessas classes, 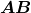 , passa a ser, então, o comprimento de
, passa a ser, então, o comprimento de 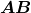 .
.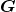 iniciou por tomar um conjunto
iniciou por tomar um conjunto 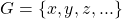 . Então, definiu-se uma relação de equivalência entre os elementos de
. Então, definiu-se uma relação de equivalência entre os elementos de  . Ou seja, uma relação que satisfaça, para quaisquer elementos
. Ou seja, uma relação que satisfaça, para quaisquer elementos  ,
, 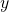 e
e  de
de  , as seguintes condições:
, as seguintes condições: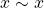 (reflexividade);
(reflexividade);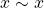 diz-se que “
diz-se que “ e
e 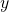 são equivalentes com respeito à Grandeza
são equivalentes com respeito à Grandeza  ”. Na interpretação do exemplo dos segmentos de reta, tem-se: “
”. Na interpretação do exemplo dos segmentos de reta, tem-se: “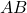 e
e 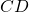 são equivalentes com respeito ao comprimento” ou simplesmente “
são equivalentes com respeito ao comprimento” ou simplesmente “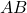 e
e 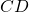 têm o mesmo comprimento” (BELLEMAIN; LIMA, 2002).
têm o mesmo comprimento” (BELLEMAIN; LIMA, 2002).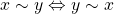 (simetria);
(simetria);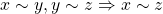 (transitividade).
(transitividade). simbolizada por
simbolizada por 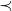 , tal que, para dois elementos quaisquer
, tal que, para dois elementos quaisquer  e
e 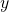 pertencentes a
pertencentes a  , ocorre uma e só uma das situações:
, ocorre uma e só uma das situações: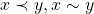 ou
ou 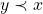 (tricotomia).
(tricotomia).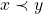 diz-se “
diz-se “ é menor do que
é menor do que 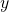 ”. No caso dos segmentos de reta
”. No caso dos segmentos de reta 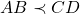 deve-se ler “
deve-se ler “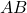 tem comprimento menor do que
tem comprimento menor do que 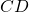 ”. A transitividade dessa relação é também suposta (BELLEMAIN; LIMA, 2002):
”. A transitividade dessa relação é também suposta (BELLEMAIN; LIMA, 2002):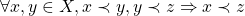 .
. no conjunto
no conjunto  :
: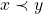 e
e 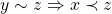 .
.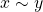 e
e 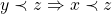 .
. permite definir o conjunto das classes de equivalência que são constituídas tomando-se, para cada elemento
permite definir o conjunto das classes de equivalência que são constituídas tomando-se, para cada elemento  em
em  , a classe
, a classe 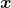 de todos os elementos equivalentes a
de todos os elementos equivalentes a  . Forma-se, então, o conjunto
. Forma-se, então, o conjunto 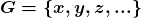 , denominado um “domínio de quantidades de Grandeza
, denominado um “domínio de quantidades de Grandeza  “. Os elementos
“. Os elementos 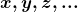 de
de  são “quantidades da Grandeza
são “quantidades da Grandeza  “, ou, nos casos em que a Grandeza
“, ou, nos casos em que a Grandeza  é subentendida, simplesmente “quantidades”. Também, chamam-se os elementos
é subentendida, simplesmente “quantidades”. Também, chamam-se os elementos 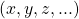 de
de  de “valores da Grandeza
de “valores da Grandeza  “, ou apenas Grandezas. No mais, quando se está lidando com mais de uma Grandeza, a expressão “domínio de quantidades da Grandeza
“, ou apenas Grandezas. No mais, quando se está lidando com mais de uma Grandeza, a expressão “domínio de quantidades da Grandeza  ” é, em geral, simplificada para “Grandeza
” é, em geral, simplificada para “Grandeza  ”, ou mesmo, “
”, ou mesmo, “ ”.
”. passam a ser comparáveis, obtendo-se uma relação de ordem total. Assim, os autores transportaram para o conjunto
passam a ser comparáveis, obtendo-se uma relação de ordem total. Assim, os autores transportaram para o conjunto  , das classes de equivalência, essa relação de ordem definida no conjunto base
, das classes de equivalência, essa relação de ordem definida no conjunto base  . Para duas classes quaisquer
. Para duas classes quaisquer 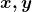 pertencentes a
pertencentes a  , definiram
, definiram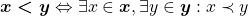 .
. e
e 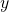 escolhidos nas respectivas classes
escolhidos nas respectivas classes 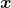 e
e 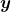 , assegurando que a relação de ordem acima está bem definida. Além disso, a igualdade
, assegurando que a relação de ordem acima está bem definida. Além disso, a igualdade 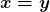 , sendo uma igualdade entre dois conjuntos, significa que todo elemento de
, sendo uma igualdade entre dois conjuntos, significa que todo elemento de 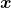 pertence a
pertence a 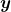 e, reciprocamente, todo elemento de
e, reciprocamente, todo elemento de 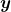 pertence a
pertence a 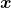 . Dessa maneira, para
. Dessa maneira, para 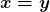 , se
, se  e
e 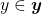 , então
, então 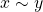 (BELLEMAIN; LIMA, 2002).
(BELLEMAIN; LIMA, 2002). e
e 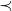 foram traduzidas pelos autores em proposições relativas ao conjunto
foram traduzidas pelos autores em proposições relativas ao conjunto  das classes e podem ser demonstradas sem dificuldades (BELLEMAIN; LIMA, 2002).
das classes e podem ser demonstradas sem dificuldades (BELLEMAIN; LIMA, 2002). no conjunto
no conjunto  é uma relação de equivalência, ou seja, é uma relação reflexiva, simétrica e transitiva.
é uma relação de equivalência, ou seja, é uma relação reflexiva, simétrica e transitiva.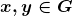 , verifica-se uma e só uma das alternativas:
, verifica-se uma e só uma das alternativas: 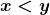 ;
; 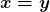 ;
; 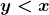 .
.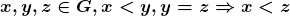 .
.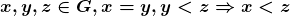 .
.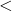 é uma relação de ordem estrita no conjunto
é uma relação de ordem estrita no conjunto  , pois, em virtude da Proposição 4, dois elementos quaisquer de
, pois, em virtude da Proposição 4, dois elementos quaisquer de  são sempre comparáveis (BELLEMAIN; LIMA, 2002).
são sempre comparáveis (BELLEMAIN; LIMA, 2002). , definindo-a, no entanto, apenas para elementos
, definindo-a, no entanto, apenas para elementos 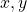 que sejam distintos. Esta última restrição reflete a impossibilidade física de se efetuar a combinação dita anteriormente com apenas um segmento de reta (BELLEMAIN; LIMA, 2002):
que sejam distintos. Esta última restrição reflete a impossibilidade física de se efetuar a combinação dita anteriormente com apenas um segmento de reta (BELLEMAIN; LIMA, 2002): define-se um elemento de
define-se um elemento de  , simbolizado por
, simbolizado por 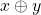 , que satisfaz as seguintes condições para qualquer
, que satisfaz as seguintes condições para qualquer 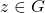 , desde que as adições estejam definidas:
, desde que as adições estejam definidas: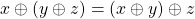 (associatividade);
(associatividade);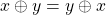 (comutatividade);
(comutatividade);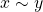 e
e 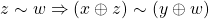 ;
;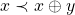 ;
;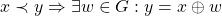 .
. das classes de equivalência de
das classes de equivalência de  relativamente à relação
relativamente à relação  , definindo uma operação binária em
, definindo uma operação binária em  , por meio dos representantes das classes de
, por meio dos representantes das classes de  . Para contornar a dificuldade na definição de
. Para contornar a dificuldade na definição de 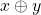 , em que é necessário supor
, em que é necessário supor 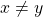 , e, além do mais, possibilitar a adição de um número qualquer de parcelas, os autores introduziram outro axioma:
, e, além do mais, possibilitar a adição de um número qualquer de parcelas, os autores introduziram outro axioma: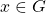 , existe um número infinito de elementos
, existe um número infinito de elementos 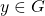 , tais que
, tais que 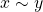 e
e 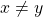 .
. possuem um número infinito de elementos. Com base no que eles admitiram anteriormente, é possível, então, definir a operação binária desejada (BELLEMAIN; LIMA, 2002):
possuem um número infinito de elementos. Com base no que eles admitiram anteriormente, é possível, então, definir a operação binária desejada (BELLEMAIN; LIMA, 2002):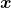 e
e 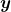 elementos de
elementos de  . Tomem-se
. Tomem-se  e
e 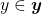 , efetue-se a adição
, efetue-se a adição 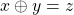 e considere-se a classe
e considere-se a classe 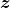 do elemento
do elemento  . Por definição,
. Por definição, 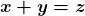 .
.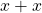 , pois o Axioma 7 permite a escolha de representantes distintos na classe
, pois o Axioma 7 permite a escolha de representantes distintos na classe 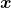 . Em seguida, foi notado que é possível transportar as propriedades da adição válidas para o conjunto base
. Em seguida, foi notado que é possível transportar as propriedades da adição válidas para o conjunto base  , para o conjunto das classes
, para o conjunto das classes  , enunciado no que se segue.
, enunciado no que se segue.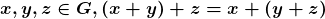 .
.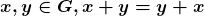 .
.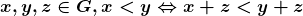 .
.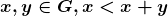 .
.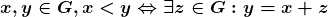 .
.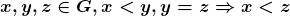 .
.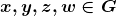 ,
,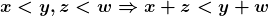 .
.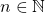 . A ideia é considerar uma operação do conjunto
. A ideia é considerar uma operação do conjunto 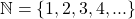 sobre o conjunto
sobre o conjunto  (BELLEMAIN; LIMA, 2002).
(BELLEMAIN; LIMA, 2002).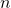 e um elemento
e um elemento 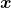 de
de  definem
definem 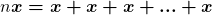 (
(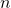 vezes).
vezes).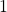 multiplicado pela classe
multiplicado pela classe 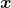 é igual a própria classe
é igual a própria classe 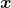 . Na segunda linha dessa definição, usando recorrência, temos à esquerda da igualdade (utilizando o leitor como referência)
. Na segunda linha dessa definição, usando recorrência, temos à esquerda da igualdade (utilizando o leitor como referência) 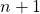 multiplicado pela classe
multiplicado pela classe 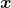 , que é igual a
, que é igual a 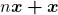 , à direita da igualdade. Note que os dois sinais de adição que aparecem nessa igualdade têm naturezas distintas e estão em mundos diferentes. No lado esquerdo, esse sinal de adição
, à direita da igualdade. Note que os dois sinais de adição que aparecem nessa igualdade têm naturezas distintas e estão em mundos diferentes. No lado esquerdo, esse sinal de adição 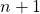 é a adição que aprendemos ao estudarmos os Axiomas de Peano, está relacionada a ideia de sucessor. Já o sinal de adição do lado direito da igualdade é o operador de classes da Definição 1.
é a adição que aprendemos ao estudarmos os Axiomas de Peano, está relacionada a ideia de sucessor. Já o sinal de adição do lado direito da igualdade é o operador de classes da Definição 1. , o conjunto
, o conjunto 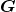 . Em outras palavras, é uma ação do monoide dos naturais com a multiplicação usual sobre o conjunto
. Em outras palavras, é uma ação do monoide dos naturais com a multiplicação usual sobre o conjunto 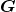 das classes de equivalência.
das classes de equivalência.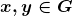 e para todo
e para todo  , são válidas as igualdades:
, são válidas as igualdades: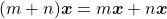 ;
;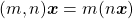 ;
;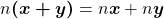 .
.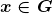 e para todo
e para todo 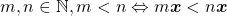 .
.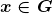 e para todo
e para todo 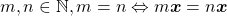 .
.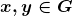 e para todo
e para todo 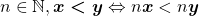 .
.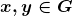 e para todo
e para todo 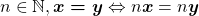 .
.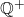 dos racionais estritamente positivos (BELLEMAIN; LIMA, 2002). Para isso, os autores introduziram a divisão de uma quantidade por um número natural e iniciaram por observar que, para cada
dos racionais estritamente positivos (BELLEMAIN; LIMA, 2002). Para isso, os autores introduziram a divisão de uma quantidade por um número natural e iniciaram por observar que, para cada 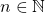 , pode ser definido um operador:
, pode ser definido um operador: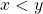 então
então 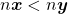 . Assim, a função
. Assim, a função 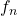 é injetiva de
é injetiva de  em
em  (BELLEMAIN; LIMA, 2002). Os autores adotaram, então, o seguinte axioma:
(BELLEMAIN; LIMA, 2002). Os autores adotaram, então, o seguinte axioma: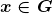 e
e 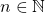 , existe
, existe 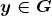 tal que
tal que 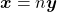 .
.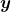 acima definido é dito a
acima definido é dito a 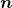 -ésima parte de
-ésima parte de 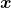 sendo simbolizado por
sendo simbolizado por 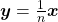 . Como a função
. Como a função 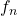 é injetiva o elemento
é injetiva o elemento 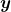 é único. Pôde-se, então, ser definido o operador
é único. Pôde-se, então, ser definido o operador 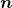 -ésima parte, a saber, a função
-ésima parte, a saber, a função 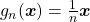 (BELLEMAIN; LIMA, 2002).
(BELLEMAIN; LIMA, 2002).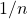 na expressão de
na expressão de 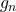 não é o número racional
não é o número racional 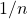 , mas apenas uma notação que caracteriza de forma conveniente o operador
, mas apenas uma notação que caracteriza de forma conveniente o operador 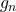 (BELLEMAIN; LIMA, 2002). A identificação deste operador com o número racional é precisamente o objetivo das etapas que se seguem da explanação dos autores. Para isso, desenvolveram regras operatórias com os coeficientes
(BELLEMAIN; LIMA, 2002). A identificação deste operador com o número racional é precisamente o objetivo das etapas que se seguem da explanação dos autores. Para isso, desenvolveram regras operatórias com os coeficientes 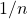 que imitam aquelas já obtidas para os coeficientes naturais. Foi preciso, no entanto, que os autores contornassem nesta etapa expressões do tipo
que imitam aquelas já obtidas para os coeficientes naturais. Foi preciso, no entanto, que os autores contornassem nesta etapa expressões do tipo 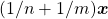 ou do tipo
ou do tipo ![Rendered by QuickLaTeX.com [(1/m)(1/n)] \boldsymbol{x}](http://blogs.multimeios.ufc.br/fernandacarmo/wp-content/ql-cache/quicklatex.com-b6f47d2d4ae1a07d689d9291f0458024_l3.png) , pois ainda não seria possível atribuir significado a tais expressões.
, pois ainda não seria possível atribuir significado a tais expressões.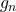 :
: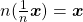 ,
,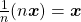 .
.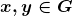 e para todo
e para todo  , tem-se:
, tem-se:![Rendered by QuickLaTeX.com \frac{1}{m} \boldsymbol{x}+ \frac{1}{n} \boldsymbol{x}= \frac{1}{mn}[(m+n) \boldsymbol{x}]](http://blogs.multimeios.ufc.br/fernandacarmo/wp-content/ql-cache/quicklatex.com-9a90f5132ec6eea41a048bf20e80f911_l3.png) ;
;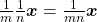 ;
;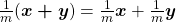 .
.![Rendered by QuickLaTeX.com mn[\frac{1}{m} \boldsymbol{x}+ \frac{1}{n} \boldsymbol{x}]=mn(\frac{1}{m} \boldsymbol{x})+mn(\frac{1}{n} \boldsymbol{x})=n[m(\frac{1}{m} \boldsymbol{x})]+m[n(\frac{1}{n} \boldsymbol{x})]=](http://blogs.multimeios.ufc.br/fernandacarmo/wp-content/ql-cache/quicklatex.com-782073b0723510604bd63d8668eab4bc_l3.png)
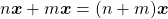 .
.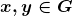 e para todo
e para todo 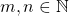 , tem-se:
, tem-se: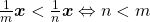 ,
,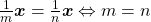 ,
,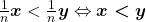 ,
,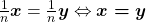 .
.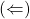 Suponha-se que
Suponha-se que 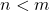 . Se não se tem
. Se não se tem 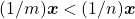 , dever-se-á ter
, dever-se-á ter 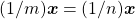 ou
ou 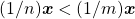 . No primeiro caso, virá
. No primeiro caso, virá 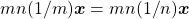 , donde resulta
, donde resulta  e, portanto,
e, portanto,  , contrariando a hipótese. No segundo caso, deduz-se que
, contrariando a hipótese. No segundo caso, deduz-se que 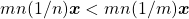 , que implica na desigualdade
, que implica na desigualdade 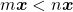 e, portanto,
e, portanto,  , o que contradiz a hipótese (BELLEMAIN; LIMA, 2002).
, o que contradiz a hipótese (BELLEMAIN; LIMA, 2002).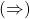 Seja
Seja 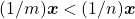 . Suponha, por absurdo, que não ocorre
. Suponha, por absurdo, que não ocorre 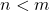 . Deverá, então ser
. Deverá, então ser  ou
ou  . No primeiro caso tem-se, de imediato,
. No primeiro caso tem-se, de imediato, 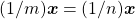 , contradizendo a hipótese. Na segunda alternativa, levando em conta a proposição direta resulta
, contradizendo a hipótese. Na segunda alternativa, levando em conta a proposição direta resulta 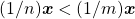 , contrariamente à hipótese. Logo,
, contrariamente à hipótese. Logo, 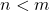 , como se queria provar (BELLEMAIN; LIMA, 2002).
, como se queria provar (BELLEMAIN; LIMA, 2002).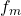 e
e 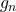 sendo
sendo  . Uma propriedade útil para essa definição foi dada na:
. Uma propriedade útil para essa definição foi dada na: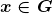 e para todo
e para todo  , tem-se
, tem-se 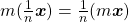 .
.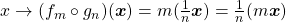 .
.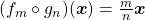 .
.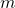 com uma divisão pelo número natural
com uma divisão pelo número natural 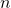 . Seguindo etapas análogas às que foram seguidas quando se tratava de
. Seguindo etapas análogas às que foram seguidas quando se tratava de 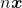 e de
e de 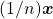 , podem ser demonstradas as proposições que se seguem.
, podem ser demonstradas as proposições que se seguem.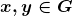 e para todo
e para todo 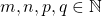 , tem-se:
, tem-se: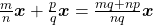 ,
,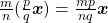 ,
,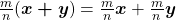 .
.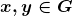 e para todo
e para todo 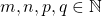 , tem-se:
, tem-se: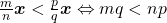 ,
,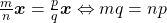 ,
,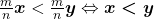 ,
,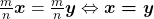 .
.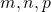 e
e  da Propriedade i) foram apresentadas da forma indicada pelo fato de que nessa exposição ainda não tinham sido atribuídos significados para relações do tipo
da Propriedade i) foram apresentadas da forma indicada pelo fato de que nessa exposição ainda não tinham sido atribuídos significados para relações do tipo 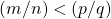 (BELLEMAIN; LIMA, 2002).
(BELLEMAIN; LIMA, 2002).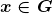 e para todo
e para todo 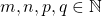 , tem-se
, tem-se 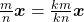 .
.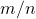 . Dado um par ordenado
. Dado um par ordenado 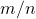 , o procedimento referido permite definir um par ordenado
, o procedimento referido permite definir um par ordenado 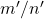 , denominado par ordenado reduzido de
, denominado par ordenado reduzido de 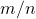 , em que
, em que 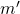 e
e 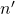 são primos entre si e
são primos entre si e 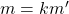 e
e 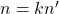 , para algum número natural
, para algum número natural 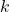 .
.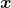 um elemento qualquer de
um elemento qualquer de  . Se
. Se 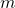 e
e 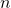 são primos entre si e se
são primos entre si e se 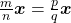 então, existe um número natural
então, existe um número natural 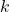 tal que
tal que 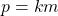 e
e 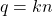 .
.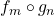 e
e 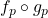 têm o mesmo efeito sobre um elemento de
têm o mesmo efeito sobre um elemento de  se, e somente se, os pares reduzidos de
se, e somente se, os pares reduzidos de 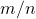 e de
e de 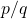 forem iguais.
forem iguais.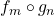 , para
, para 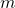 e
e 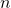 arbitrários, e que nesse conjunto se possa definir a relação de equivalência induzida pela Proposição 26. Com isso, foi possível definir um espaço
arbitrários, e que nesse conjunto se possa definir a relação de equivalência induzida pela Proposição 26. Com isso, foi possível definir um espaço 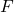 de classes de operadores sobre
de classes de operadores sobre  denominadas operadores de fracionamento ou operadores racionais (BELLEMAIN; LIMA, 2002). Os autores tomaram, então, nesse espaço, as operações de adição e decomposição de classes de operadores induzidas pelas igualdades válidas para quaisquer
denominadas operadores de fracionamento ou operadores racionais (BELLEMAIN; LIMA, 2002). Os autores tomaram, então, nesse espaço, as operações de adição e decomposição de classes de operadores induzidas pelas igualdades válidas para quaisquer 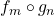 e
e 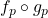 :
:![Rendered by QuickLaTeX.com [(f_{m} \circ g_{n})+(f_{p} \circ g_{p})] (\boldsymbol{x})= \frac{m}{n} \boldsymbol{x}+ \frac{p}{q} \boldsymbol{x}= \frac{mq+np}{nq} \boldsymbol{x}](http://blogs.multimeios.ufc.br/fernandacarmo/wp-content/ql-cache/quicklatex.com-ed520c97209af878bd70c801e3c6448c_l3.png) ,
,![Rendered by QuickLaTeX.com [(f_{m} \circ g_{n}) \circ (f_{p} \circ g_{p})] (\boldsymbol{x})= \frac{m}{n} (\frac{p}{q} \boldsymbol{x})= \frac{mp}{nq}\boldsymbol{x}](http://blogs.multimeios.ufc.br/fernandacarmo/wp-content/ql-cache/quicklatex.com-2c0936e7e713c659e4d651dd95cd079a_l3.png) .
.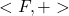 , constituído pelo conjunto
, constituído pelo conjunto 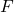 e pela operação de adição, é um semigrupo comutativo. Igualmente, é um semigrupo comutativo o espaço
e pela operação de adição, é um semigrupo comutativo. Igualmente, é um semigrupo comutativo o espaço 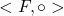 e, além disso, é válida a distributividade da operação de composição relativamente à adição (BELLEMAIN, LIMA, 2002).
e, além disso, é válida a distributividade da operação de composição relativamente à adição (BELLEMAIN, LIMA, 2002).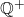 dos racionais estritamente positivos, munido das operações usuais de adição e multiplicação de racionais. Verifica-se, por meio de uma demonstração simples, que existe um isomorfismo entre as estruturas
dos racionais estritamente positivos, munido das operações usuais de adição e multiplicação de racionais. Verifica-se, por meio de uma demonstração simples, que existe um isomorfismo entre as estruturas 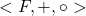 e
e 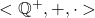 . Em outros termos, é possível provar a existência de uma identificação entre o espaço de operadores de fracionamento e os números racionais estritamente positivos.
. Em outros termos, é possível provar a existência de uma identificação entre o espaço de operadores de fracionamento e os números racionais estritamente positivos.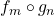 são primos entre si, ou seja, são pares ordenados reduzidos; além disso para tornar mais leve a linguagem, dizemos o “operador
são primos entre si, ou seja, são pares ordenados reduzidos; além disso para tornar mais leve a linguagem, dizemos o “operador 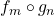 ” em vez de “a classe do operador
” em vez de “a classe do operador 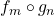 ”.
”.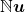 , constituída pelos múltiplos naturais de uma unidade
, constituída pelos múltiplos naturais de uma unidade 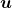 . Assim, essa estrutura inclui o próprio sistema dos números naturais, que podem ser entendidos como quantidades de uma Grandeza ou, simplesmente, como Grandezas. Desse modo, a unidade usada seria o número 1. Esse é o modelo abstrato das chamadas Grandezas discretas.
. Assim, essa estrutura inclui o próprio sistema dos números naturais, que podem ser entendidos como quantidades de uma Grandeza ou, simplesmente, como Grandezas. Desse modo, a unidade usada seria o número 1. Esse é o modelo abstrato das chamadas Grandezas discretas.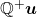 , constituído pelos múltiplos,
, constituído pelos múltiplos, 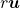 , de uma dada quantidade
, de uma dada quantidade 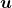 , escolhida arbitrariamente como unidade de medida.
, escolhida arbitrariamente como unidade de medida.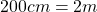 em que expressa igualdade entre duas quantidades da Grandeza comprimento, isto é, uma igualdade entre dois comprimentos. Ou seja, é uma igualdade que expressa um mesmo comprimento representado em duas unidades diferentes, no caso, o centímetro e o metro. Ou ainda,
em que expressa igualdade entre duas quantidades da Grandeza comprimento, isto é, uma igualdade entre dois comprimentos. Ou seja, é uma igualdade que expressa um mesmo comprimento representado em duas unidades diferentes, no caso, o centímetro e o metro. Ou ainda, 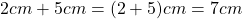 , que envolve a operação de adição de duas quantidades, um conceito primitivo (sem definição, portanto) na estrutura matemática que foi apresentada. A validade dessa cadeia de igualdades resulta das regras adotadas como axiomas no mencionado sistema lógico, bem como da definição de
, que envolve a operação de adição de duas quantidades, um conceito primitivo (sem definição, portanto) na estrutura matemática que foi apresentada. A validade dessa cadeia de igualdades resulta das regras adotadas como axiomas no mencionado sistema lógico, bem como da definição de 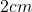 e
e 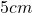 , cada um deles sendo um produto de um número racional por uma quantidade. Do ponto de vista formal, a álgebra utilizada nesse exemplo é inteiramente análoga à álgebra dos polinômios, na qual
, cada um deles sendo um produto de um número racional por uma quantidade. Do ponto de vista formal, a álgebra utilizada nesse exemplo é inteiramente análoga à álgebra dos polinômios, na qual 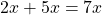 .
.