2.3.2 Medida
Trazemos a definição de Medida como está em Halmos (1950, p. 30-31, tradução nossa), no seu livro Measure Theory.
Uma função conjunto é uma função cujo domínio é uma classe de conjuntos. Uma função conjunto de valor real estendida 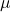 definida em uma classe
definida em uma classe 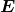 de conjuntos é aditiva se, sempre que
de conjuntos é aditiva se, sempre que
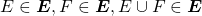 e
e 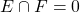 , então
, então
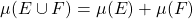 .
.
Uma função conjunto de valor real estendida 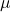 definida em uma classe
definida em uma classe 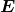 é finitamente aditiva se, para cada classe finita e disjunta
é finitamente aditiva se, para cada classe finita e disjunta 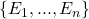 de conjuntos em
de conjuntos em 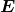 cuja união também está em
cuja união também está em 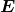 , temos
, temos
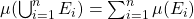 .
.
Uma função conjunto de valor real estendida 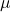 definida em uma classe
definida em uma classe 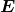 é contavelmente aditiva se, para cada sequência disjunta
é contavelmente aditiva se, para cada sequência disjunta 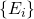 de conjuntos em
de conjuntos em 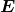 cuja união também está em
cuja união também está em 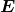 , temos
, temos
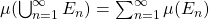 .
.
Uma Medida é uma função conjunto 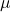 de valor real estendida, não negativa e contavelmente aditiva, definida em um anel
de valor real estendida, não negativa e contavelmente aditiva, definida em um anel 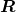 , e tal que
, e tal que 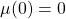 . Em vista da identidade,
. Em vista da identidade,
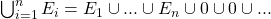 ,
,
uma Medida é sempre finitamente aditiva.
Apenas para lembrar, um anel (ou anel Booleano) de conjuntos é uma classe 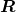 não vazia de conjuntos tais que
não vazia de conjuntos tais que
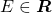 e
e 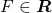 , então
, então
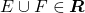 e
e 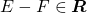 .
.
Ou seja, um anel é uma classe de conjuntos não vazia, fechada sob a formação de uniões e diferenças.
Vejamos um exemplo trivial de uma medida:
Seja 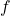 uma função não negativa de valor real estendida dos pontos de um conjunto
uma função não negativa de valor real estendida dos pontos de um conjunto 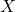 . Seja o anel
. Seja o anel 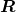 composto por todos os subconjuntos finitos de
composto por todos os subconjuntos finitos de 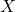 ; define-se
; define-se 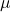 por
por
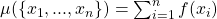 e
e 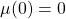 .
.
Outros exemplos menos triviais:
Se 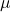 é uma Medida em um anel
é uma Medida em um anel 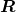 , um conjunto
, um conjunto 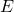 em
em 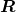 é dito ter medida finita se
é dito ter medida finita se 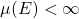 ; a Medida de
; a Medida de 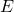 é
é  -finita se existe uma sequência
-finita se existe uma sequência 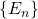 de conjuntos em
de conjuntos em 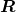 tal que
tal que
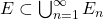 e
e 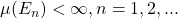 .
.
Se a Medida de cada conjunto 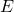 em
em 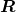 é finita (ou
é finita (ou 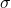 -finita), a Medida
-finita), a Medida 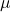 é chamada finita (ou
é chamada finita (ou  -finita) em
-finita) em 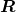 . Se
. Se 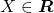 (ou seja, se
(ou seja, se 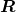 é uma álgebra) e
é uma álgebra) e 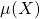 é finito ou
é finito ou 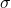 -finito, então
-finito, então 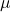 é chamado de totalmente finito ou totalmente
é chamado de totalmente finito ou totalmente  -finito, respectivamente. A Medida
-finito, respectivamente. A Medida 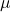 é chamada completa se as condições
é chamada completa se as condições
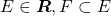 e
e 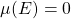
implica que 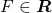 .
.

2.3.1 Grandeza
|

Início
|

2.3.3 Medida de Área
|
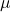 definida em uma classe
definida em uma classe 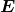 de conjuntos é aditiva se, sempre que
de conjuntos é aditiva se, sempre que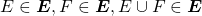 e
e 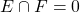 , então
, então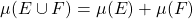 .
.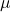 definida em uma classe
definida em uma classe 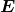 é finitamente aditiva se, para cada classe finita e disjunta
é finitamente aditiva se, para cada classe finita e disjunta 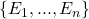 de conjuntos em
de conjuntos em 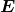 cuja união também está em
cuja união também está em 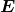 , temos
, temos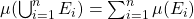 .
.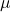 definida em uma classe
definida em uma classe 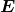 é contavelmente aditiva se, para cada sequência disjunta
é contavelmente aditiva se, para cada sequência disjunta 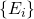 de conjuntos em
de conjuntos em 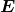 cuja união também está em
cuja união também está em 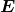 , temos
, temos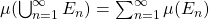 .
.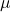 de valor real estendida, não negativa e contavelmente aditiva, definida em um anel
de valor real estendida, não negativa e contavelmente aditiva, definida em um anel 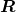 , e tal que
, e tal que 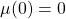 . Em vista da identidade,
. Em vista da identidade,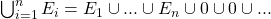 ,
,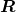 não vazia de conjuntos tais que
não vazia de conjuntos tais que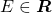 e
e 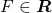 , então
, então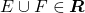 e
e 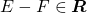 .
.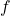 uma função não negativa de valor real estendida dos pontos de um conjunto
uma função não negativa de valor real estendida dos pontos de um conjunto 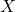 . Seja o anel
. Seja o anel 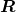 composto por todos os subconjuntos finitos de
composto por todos os subconjuntos finitos de 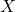 ; define-se
; define-se 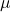 por
por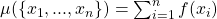 e
e 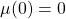 .
.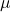 é uma Medida em um anel
é uma Medida em um anel 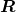 , um conjunto
, um conjunto 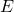 em
em 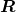 é dito ter medida finita se
é dito ter medida finita se 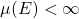 ; a Medida de
; a Medida de 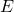 é
é  -finita se existe uma sequência
-finita se existe uma sequência 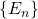 de conjuntos em
de conjuntos em 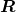 tal que
tal que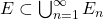 e
e 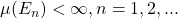 .
.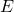 em
em 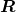 é finita (ou
é finita (ou 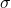 -finita), a Medida
-finita), a Medida 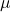 é chamada finita (ou
é chamada finita (ou  -finita) em
-finita) em 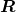 . Se
. Se 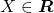 (ou seja, se
(ou seja, se 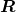 é uma álgebra) e
é uma álgebra) e 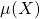 é finito ou
é finito ou 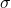 -finito, então
-finito, então 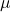 é chamado de totalmente finito ou totalmente
é chamado de totalmente finito ou totalmente  -finito, respectivamente. A Medida
-finito, respectivamente. A Medida 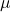 é chamada completa se as condições
é chamada completa se as condições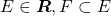 e
e 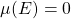
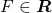 .
.