Pular para o conteúdo
2.3.3 Medida de Área
Utilizamos Lima (1995, p. 51-53) e Bellemain e Lima (2002) para apresentar uma estrutura matemática para o conceito de Área de superfícies planas, para o processo de medir área. Inicialmente, os autores convencionaram que o termo superfície significa um conjunto limitado do plano euclidiano. O ponto de partida foi definir uma função  , chamada função área, em um conjunto
, chamada função área, em um conjunto  de superfícies, com valores em
de superfícies, com valores em 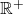 (os números reais não negativos) e que possua certas propriedades julgadas apropriadas para caracterizarem a Grandeza área, a saber:
(os números reais não negativos) e que possua certas propriedades julgadas apropriadas para caracterizarem a Grandeza área, a saber:
i) positividade: se  tem interior não vazio,
tem interior não vazio, 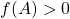 ;
;
Ou seja, uma figura de interior não vazio tem Área positiva (BELLEMAIN; LIMA, 2002).
ii) aditividade: 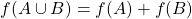 , se
, se  e
e  são “quase disjuntos”, isto é, se
são “quase disjuntos”, isto é, se  contém, quando muito, pontos de suas fronteiras;
contém, quando muito, pontos de suas fronteiras;
Isto é, se duas figuras  e
e  que têm em comum no máximo pontos de suas fronteiras, então a Área da figura
que têm em comum no máximo pontos de suas fronteiras, então a Área da figura 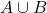 , união de
, união de  e
e  , é a soma da Área de
, é a soma da Área de  com a Área de
com a Área de  (BELLEMAIN; LIMA, 2002).
(BELLEMAIN; LIMA, 2002).
iii) invariância por isometrias: se uma figura plana  é transformada em outra,
é transformada em outra,  , de modo que a distância entre dois pontos quaisquer de
, de modo que a distância entre dois pontos quaisquer de  fica inalterada em
fica inalterada em  , então,
, então, 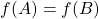 .
.
Em outros termos, se uma figura plana  é transformada em outra,
é transformada em outra,  , de modo que a distância entre dois pontos quaisquer de
, de modo que a distância entre dois pontos quaisquer de  fica inalterada em
fica inalterada em  , então,
, então,  e
e  têm a mesma Área (BELLEMAIN; LIMA, 2002).
têm a mesma Área (BELLEMAIN; LIMA, 2002).
Adotadas as propriedades acima, os autores impõem a questão matemática de caracterizar o domínio  da função
da função  . Eles destacaram que, se são exigidas as condições acima para a função área, não é possível medir todo subconjunto do plano. Desse modo, é preciso saber quais superfícies são mensuráveis por
. Eles destacaram que, se são exigidas as condições acima para a função área, não é possível medir todo subconjunto do plano. Desse modo, é preciso saber quais superfícies são mensuráveis por  . Esse é um tema próprio da Teoria da Medida, que é contornado pelos autores ao convencionarem que
. Esse é um tema próprio da Teoria da Medida, que é contornado pelos autores ao convencionarem que  satisfaz a axiomas que asseguram que as figuras planas da matemática escolar são mensuráveis, entre outros:
satisfaz a axiomas que asseguram que as figuras planas da matemática escolar são mensuráveis, entre outros:
Axioma 1. Se 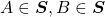 , então
, então 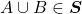 e
e 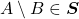 .
.
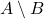 representa a diferença dos conjuntos
representa a diferença dos conjuntos  e
e  , que é o conjunto dos elementos de
, que é o conjunto dos elementos de  que não estão em
que não estão em  (LIMA, 1995).
(LIMA, 1995).
Axioma 2. Os quadrados pertencem a  .
.
Axioma 3. Se  é limitado e
é limitado e 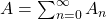 com
com 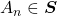 , para todo
, para todo 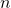 , então,
, então, 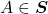 .
.
Os autores tomaram, então, um quadrado 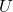 , para superfície unitária. Para quadrado unitário é, em geral, escolhido aquele cujo lado é um segmento unitário, isto é, de comprimento 1. Portanto, sejam
, para superfície unitária. Para quadrado unitário é, em geral, escolhido aquele cujo lado é um segmento unitário, isto é, de comprimento 1. Portanto, sejam 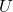 esse quadrado e
esse quadrado e 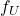 a função área tal que
a função área tal que 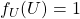 . Estabelece-se, então, a terminologia:
. Estabelece-se, então, a terminologia: 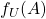 , é a Medida de Área da superfície
, é a Medida de Área da superfície  , na unidade de medida
, na unidade de medida 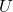 . Com isso, uma figura
. Com isso, uma figura  que se possa construir como união finita de quadrados unitários quase disjuntos pertence a
que se possa construir como união finita de quadrados unitários quase disjuntos pertence a  e o valor
e o valor 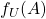 é o número de quadrados unitários contidos na figura (LIMA, 1995).
é o número de quadrados unitários contidos na figura (LIMA, 1995).
Na etapa seguinte da construção da função 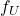 , os autores ressaltaram um instrumento fundamental que são as fórmulas de área. Se
, os autores ressaltaram um instrumento fundamental que são as fórmulas de área. Se  é um quadrado qualquer cujo lado tem comprimento de medida inteira
é um quadrado qualquer cujo lado tem comprimento de medida inteira  , pode-se ver, de imediato, que
, pode-se ver, de imediato, que 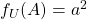 . Por subdivisão apropriada do lado do quadrado
. Por subdivisão apropriada do lado do quadrado 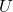 , deduz-se que, se
, deduz-se que, se  tem lado racional
tem lado racional  , também será
, também será 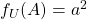 . Esta mesma fórmula vale mesmo se
. Esta mesma fórmula vale mesmo se  é irracional. Para se deduzir tal fato, no entanto, é necessário que se adote mais uma propriedade a ser verificada pela função
é irracional. Para se deduzir tal fato, no entanto, é necessário que se adote mais uma propriedade a ser verificada pela função 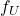 . A função
. A função 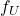 que o satisfaça poderá ser calculada em quadrados de lado com medida irracional e, mais geralmente ainda, em superfícies de fronteiras curvas. Uma formulação possível é:
que o satisfaça poderá ser calculada em quadrados de lado com medida irracional e, mais geralmente ainda, em superfícies de fronteiras curvas. Uma formulação possível é:
Axioma 4. Aditividade para uniões enumeráveis: se 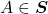 e
e 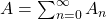 com
com 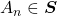 e
e 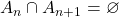 , então,
, então, 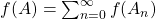 . (Expressão da Área como a soma de uma série).
. (Expressão da Área como a soma de uma série).
O cálculo do valor 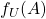 envolve a passagem ao limite de uma sequência de valores que são as somas parciais da série
envolve a passagem ao limite de uma sequência de valores que são as somas parciais da série 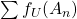 , onde
, onde 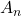 é uma das figuras que compõem
é uma das figuras que compõem  . Dessa forma surge o conceito de Área aproximada de uma superfície. O valor
. Dessa forma surge o conceito de Área aproximada de uma superfície. O valor 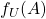 é, na prática, obtido pelo valor de somas parciais de
é, na prática, obtido pelo valor de somas parciais de 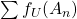 com a aproximação desejada (LIMA, 1995).
com a aproximação desejada (LIMA, 1995).
Tais axiomas permitem, por outro lado, a demonstração de que uma função área 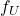 satisfazendo às condições acima referidas está definida em todos os quadrados, triângulos e em todas as superfícies que se decompõem em uniões finitas de triângulos cujos interiores sejam disjuntos dois a dois. Em suma, em toda superfície poligonal. Mais ainda, uma figura plana
satisfazendo às condições acima referidas está definida em todos os quadrados, triângulos e em todas as superfícies que se decompõem em uniões finitas de triângulos cujos interiores sejam disjuntos dois a dois. Em suma, em toda superfície poligonal. Mais ainda, uma figura plana  , mesmo não poligonal, isto é, com fronteiras curvas, que pode ser definida como união enumerável de superfícies mensuráveis, é mensurável (LIMA, 1995).
, mesmo não poligonal, isto é, com fronteiras curvas, que pode ser definida como união enumerável de superfícies mensuráveis, é mensurável (LIMA, 1995).
O autor destaca que se a superfície unitária for mudada, é possível deduzir que a função 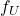 , definida em
, definida em  da forma indicada acima é única. Para isso, os autores consideraram, então,
da forma indicada acima é única. Para isso, os autores consideraram, então,  uma função área, definida em
uma função área, definida em  (satisfazendo, então, aos axiomas de positividade, aditividade e invariância por isometrias) tal que
(satisfazendo, então, aos axiomas de positividade, aditividade e invariância por isometrias) tal que 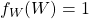 . A superfície
. A superfície 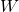 é uma nova superfície unitária. Seja
é uma nova superfície unitária. Seja 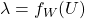 e tome a função
e tome a função 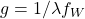 . Vemos que
. Vemos que 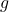 é também uma função área definida em
é também uma função área definida em  . Temos, portanto,
. Temos, portanto, 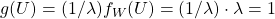 . Mas sabemos que a única função área que atende a essas condições é
. Mas sabemos que a única função área que atende a essas condições é 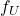 . Logo,
. Logo, 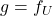 , isto é,
, isto é, 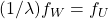 e, portanto,
e, portanto, 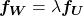 . Isto é, dadas duas funções área quaisquer,
. Isto é, dadas duas funções área quaisquer, 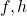 , definidas em
, definidas em  , elas diferem apenas por um fator de proporcionalidade. A questão que o autor põe neste ponto é a de explicitar uma estrutura matemática na qual se defina o termo área.
, elas diferem apenas por um fator de proporcionalidade. A questão que o autor põe neste ponto é a de explicitar uma estrutura matemática na qual se defina o termo área.
Dada uma função área  , definida em
, definida em  , verificamos sua sobrejeção, isto é, dado um valor real positivo
, verificamos sua sobrejeção, isto é, dado um valor real positivo 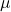 , existe uma superfície
, existe uma superfície  , tal que
, tal que 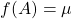 . Mas
. Mas  não é injetiva, pois há um conjunto de superfícies de
não é injetiva, pois há um conjunto de superfícies de  , representado por
, representado por 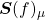 , tal que, para toda superfície
, tal que, para toda superfície  em
em 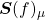 , tem-se
, tem-se 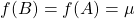 (LIMA, 1995).
(LIMA, 1995).
O conjunto das superfícies mensuráveis  pode ser dividido em classes disjuntas. Além disso, essas classes de equivalência não dependem da função área escolhida. Em outras palavras, partir de outra função área,
pode ser dividido em classes disjuntas. Além disso, essas classes de equivalência não dependem da função área escolhida. Em outras palavras, partir de outra função área, 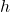 , (que se sabe, é igual a
, (que se sabe, é igual a 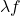 , para algum
, para algum 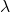 ), podemos ver que
), podemos ver que 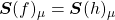 , para todo
, para todo 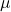 . Concluímos que
. Concluímos que  fica dividido em classes disjuntas
fica dividido em classes disjuntas 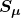 . O conjunto dessas classes,
. O conjunto dessas classes, 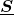 , é o conjunto das áreas. Dada uma superfície
, é o conjunto das áreas. Dada uma superfície  , sua classe,
, sua classe, 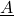 , é a Área
, é a Área 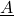 , isto é, o conjunto de todas as superfícies que têm a mesma Área que
, isto é, o conjunto de todas as superfícies que têm a mesma Área que  , quando medidas por qualquer função área (LIMA, 1995).
, quando medidas por qualquer função área (LIMA, 1995).
Nesse conjunto de classes, 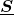 constituído, os autores puderam definir uma relação de ordem e duas operações, a adição de duas classes e a multiplicação de uma classe por um número, que satisfazem a propriedades análogas às de um espaço vetorial unidimensional sobre os reais. O conjunto
constituído, os autores puderam definir uma relação de ordem e duas operações, a adição de duas classes e a multiplicação de uma classe por um número, que satisfazem a propriedades análogas às de um espaço vetorial unidimensional sobre os reais. O conjunto 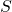 é uma estrutura matemática que permite o tratamento abstrato do conceito de Área, sendo um caso particular de um “domínio de quantidades”.
é uma estrutura matemática que permite o tratamento abstrato do conceito de Área, sendo um caso particular de um “domínio de quantidades”.
2.3.3.1 Cálculo de Áreas: Integral de Riemann
Para rever a introdução do conceito de Integral de Riemann, utilizado no cálculo de Áreas, utilizamos Guidorizzi (2001, p. 302-311).
Sejam  uma função definida em
uma função definida em ![Rendered by QuickLaTeX.com [a, b]](https://blogs.multimeios.ufc.br/fernandacarmo/wp-content/ql-cache/quicklatex.com-b28ebca9266518f1a778b4a4b102a2e1_l3.png) e
e 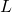 um número real. Dizemos que
um número real. Dizemos que 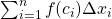 tende a
tende a 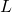 , quando
, quando 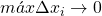 , e escrevemos
, e escrevemos 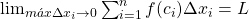 se, para todo
se, para todo 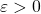 , existir um
, existir um 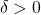 que só dependa de
que só dependa de  mas não da particular escolha dos
mas não da particular escolha dos 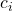 , tal que
, tal que 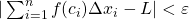 para toda partição
para toda partição 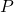 de
de ![Rendered by QuickLaTeX.com [a, b]](https://blogs.multimeios.ufc.br/fernandacarmo/wp-content/ql-cache/quicklatex.com-b28ebca9266518f1a778b4a4b102a2e1_l3.png) , com
, com 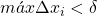 .
.
Tal número 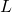 , que quando existe é único, denomina-se integral de Riemann de
, que quando existe é único, denomina-se integral de Riemann de  em
em ![Rendered by QuickLaTeX.com [a, b]](https://blogs.multimeios.ufc.br/fernandacarmo/wp-content/ql-cache/quicklatex.com-b28ebca9266518f1a778b4a4b102a2e1_l3.png) e indica-se por
e indica-se por 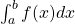 . Então, por definição
. Então, por definição 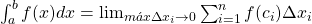 .
.
Se 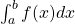 existe, então diremos que
existe, então diremos que  é integrável segundo Riemann em
é integrável segundo Riemann em ![Rendered by QuickLaTeX.com [a, b]](https://blogs.multimeios.ufc.br/fernandacarmo/wp-content/ql-cache/quicklatex.com-b28ebca9266518f1a778b4a4b102a2e1_l3.png) .
.
Ainda por definição, 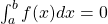 e
e 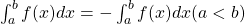 .
.
Teorema. Sejam 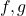 integráveis em
integráveis em ![Rendered by QuickLaTeX.com [a, b]](https://blogs.multimeios.ufc.br/fernandacarmo/wp-content/ql-cache/quicklatex.com-b28ebca9266518f1a778b4a4b102a2e1_l3.png) e
e 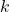 uma constante. Então,
uma constante. Então,
a) 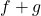 é integrável em
é integrável em ![Rendered by QuickLaTeX.com [a, b]](https://blogs.multimeios.ufc.br/fernandacarmo/wp-content/ql-cache/quicklatex.com-b28ebca9266518f1a778b4a4b102a2e1_l3.png) e
e
![Rendered by QuickLaTeX.com \int_{a}^{b}[f(x)+g(x)]dx=\int_{a}^{b}f(x)dx+ \int_{a}^{b}g(x)dx](https://blogs.multimeios.ufc.br/fernandacarmo/wp-content/ql-cache/quicklatex.com-6e260d20f5a8ba7a0b946c954ddbf0e1_l3.png) .
.
b) 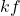 é integrável em
é integrável em ![Rendered by QuickLaTeX.com [a, b]](https://blogs.multimeios.ufc.br/fernandacarmo/wp-content/ql-cache/quicklatex.com-b28ebca9266518f1a778b4a4b102a2e1_l3.png) e
e 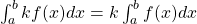 .
.
c) Se 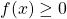 em
em ![Rendered by QuickLaTeX.com [a, b]](https://blogs.multimeios.ufc.br/fernandacarmo/wp-content/ql-cache/quicklatex.com-b28ebca9266518f1a778b4a4b102a2e1_l3.png) , então
, então 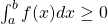 .
.
d) Se ![Rendered by QuickLaTeX.com c \in \; ]a, b[](https://blogs.multimeios.ufc.br/fernandacarmo/wp-content/ql-cache/quicklatex.com-730fbed4fd42c6b90340168430b182ce_l3.png) e
e  é integrável em
é integrável em ![Rendered by QuickLaTeX.com [a, c]](https://blogs.multimeios.ufc.br/fernandacarmo/wp-content/ql-cache/quicklatex.com-232b87f588bd0f107432d1283d8d6007_l3.png) e em
e em ![Rendered by QuickLaTeX.com [c, b]](https://blogs.multimeios.ufc.br/fernandacarmo/wp-content/ql-cache/quicklatex.com-41025a54faddc768ddcc34d10fbe66aa_l3.png) então
então
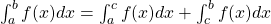 .
.
Seja  contínua em
contínua em ![Rendered by QuickLaTeX.com [a, b]](https://blogs.multimeios.ufc.br/fernandacarmo/wp-content/ql-cache/quicklatex.com-b28ebca9266518f1a778b4a4b102a2e1_l3.png) , com
, com 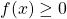 em
em ![Rendered by QuickLaTeX.com [a, b]](https://blogs.multimeios.ufc.br/fernandacarmo/wp-content/ql-cache/quicklatex.com-b28ebca9266518f1a778b4a4b102a2e1_l3.png) . Podemos definir a Área do conjunto
. Podemos definir a Área do conjunto  do plano limitado pelas retas
do plano limitado pelas retas  ,
, 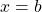 ,
, 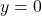 e pelo gráfico de
e pelo gráfico de 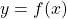 .
.
Seja, então, 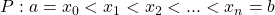 uma partição de
uma partição de ![Rendered by QuickLaTeX.com [a, b]](https://blogs.multimeios.ufc.br/fernandacarmo/wp-content/ql-cache/quicklatex.com-b28ebca9266518f1a778b4a4b102a2e1_l3.png) e sejam
e sejam 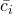 e
e 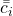 em
em ![Rendered by QuickLaTeX.com [x_{i-1}, x_{i}]](https://blogs.multimeios.ufc.br/fernandacarmo/wp-content/ql-cache/quicklatex.com-a0eeadd798a1ae81be66ce94f3679ca1_l3.png) tais que
tais que 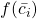 é o valor mínimo e
é o valor mínimo e 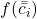 o valor máximo de
o valor máximo de  em
em ![Rendered by QuickLaTeX.com [x_{i-1}, x_{i}]](https://blogs.multimeios.ufc.br/fernandacarmo/wp-content/ql-cache/quicklatex.com-a0eeadd798a1ae81be66ce94f3679ca1_l3.png) . Uma definição para a Área de
. Uma definição para a Área de  deverá implicar que a soma de Riemann
deverá implicar que a soma de Riemann 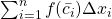 seja uma aproximação por falta da Área de
seja uma aproximação por falta da Área de  e que
e que 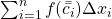 seja uma aproximação por excesso, isto é,
seja uma aproximação por excesso, isto é, 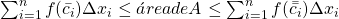 .
.
Como as somas de Riemann mencionadas tendem a 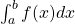 , quando
, quando 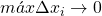 , nada mais natural do que definir a Área de
, nada mais natural do que definir a Área de  por
por 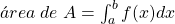 .
.
Da mesma forma define-se Área de  no caso em que
no caso em que  é uma função integrável qualquer, com
é uma função integrável qualquer, com 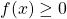 em
em ![Rendered by QuickLaTeX.com [a, b]](https://blogs.multimeios.ufc.br/fernandacarmo/wp-content/ql-cache/quicklatex.com-b28ebca9266518f1a778b4a4b102a2e1_l3.png) .
.
2.3.3.2 Cálculo de Volumes: Aplicações da Integral
Também trazemos Guidorizzi (2001, p. 411-412) para introduzir cálculo de Volumes utilizando integral.
Sabendo que ![Rendered by QuickLaTeX.com \pi \int_{a}^{b} [f(x)]^{2} dx](https://blogs.multimeios.ufc.br/fernandacarmo/wp-content/ql-cache/quicklatex.com-47d59ce87fefac0352e15a90d870d70b_l3.png) é a fórmula que fornece o Volume do sólido de revolução obtido pela rotação, em torno do eixo
é a fórmula que fornece o Volume do sólido de revolução obtido pela rotação, em torno do eixo  , do conjunto
, do conjunto 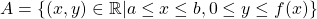 . Observemos que
. Observemos que ![Rendered by QuickLaTeX.com A(x)= \pi [f(x)]^{2}](https://blogs.multimeios.ufc.br/fernandacarmo/wp-content/ql-cache/quicklatex.com-1b163a2cfa63619bd76f2efd16e6a09e_l3.png) é a Área de interseção do sólido com o plano perpendicular ao eixo
é a Área de interseção do sólido com o plano perpendicular ao eixo  e passando pelo ponto de abcissa
e passando pelo ponto de abcissa  . Assim, o Volume mencionado anteriormente pode ser colocado na forma
. Assim, o Volume mencionado anteriormente pode ser colocado na forma
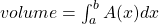 .
.
Seja, portanto,  um sólido qualquer, não necessariamente de revolução e seja
um sólido qualquer, não necessariamente de revolução e seja  um eixo escolhido arbitrariamente. Suponhamos que o sólido esteja compreendido entre dois planos perpendiculares a
um eixo escolhido arbitrariamente. Suponhamos que o sólido esteja compreendido entre dois planos perpendiculares a  , que interceptam o eixo
, que interceptam o eixo  em
em  e em
e em 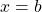 . Seja
. Seja 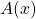 a Área de interseção do sólido com o plano perpendicular a
a Área de interseção do sólido com o plano perpendicular a  no ponto de abscissa
no ponto de abscissa  . Suponhamos que a função
. Suponhamos que a função 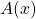 seja integrável em
seja integrável em ![Rendered by QuickLaTeX.com [a, b]](https://blogs.multimeios.ufc.br/fernandacarmo/wp-content/ql-cache/quicklatex.com-b28ebca9266518f1a778b4a4b102a2e1_l3.png) . Definimos, então, o Volume do sólido por
. Definimos, então, o Volume do sólido por
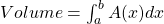 .
.
Exposto o referencial teórico, no capítulo seguinte descrevemos o percurso metodológico da pesquisa.

2.3.2 Medida
|

Início
|

3 Metodologia
|
 , chamada função área, em um conjunto
, chamada função área, em um conjunto  de superfícies, com valores em
de superfícies, com valores em 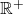 (os números reais não negativos) e que possua certas propriedades julgadas apropriadas para caracterizarem a Grandeza área, a saber:
(os números reais não negativos) e que possua certas propriedades julgadas apropriadas para caracterizarem a Grandeza área, a saber: tem interior não vazio,
tem interior não vazio, 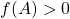 ;
;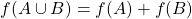 , se
, se  e
e  são “quase disjuntos”, isto é, se
são “quase disjuntos”, isto é, se  contém, quando muito, pontos de suas fronteiras;
contém, quando muito, pontos de suas fronteiras; e
e  que têm em comum no máximo pontos de suas fronteiras, então a Área da figura
que têm em comum no máximo pontos de suas fronteiras, então a Área da figura 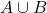 , união de
, união de  e
e  , é a soma da Área de
, é a soma da Área de  com a Área de
com a Área de  (BELLEMAIN; LIMA, 2002).
(BELLEMAIN; LIMA, 2002). é transformada em outra,
é transformada em outra,  , de modo que a distância entre dois pontos quaisquer de
, de modo que a distância entre dois pontos quaisquer de  fica inalterada em
fica inalterada em  , então,
, então, 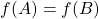 .
. é transformada em outra,
é transformada em outra,  , de modo que a distância entre dois pontos quaisquer de
, de modo que a distância entre dois pontos quaisquer de  fica inalterada em
fica inalterada em  , então,
, então,  e
e  têm a mesma Área (BELLEMAIN; LIMA, 2002).
têm a mesma Área (BELLEMAIN; LIMA, 2002). da função
da função  . Eles destacaram que, se são exigidas as condições acima para a função área, não é possível medir todo subconjunto do plano. Desse modo, é preciso saber quais superfícies são mensuráveis por
. Eles destacaram que, se são exigidas as condições acima para a função área, não é possível medir todo subconjunto do plano. Desse modo, é preciso saber quais superfícies são mensuráveis por  . Esse é um tema próprio da Teoria da Medida, que é contornado pelos autores ao convencionarem que
. Esse é um tema próprio da Teoria da Medida, que é contornado pelos autores ao convencionarem que  satisfaz a axiomas que asseguram que as figuras planas da matemática escolar são mensuráveis, entre outros:
satisfaz a axiomas que asseguram que as figuras planas da matemática escolar são mensuráveis, entre outros: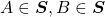 , então
, então 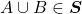 e
e 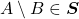 .
.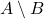 representa a diferença dos conjuntos
representa a diferença dos conjuntos  e
e  , que é o conjunto dos elementos de
, que é o conjunto dos elementos de  que não estão em
que não estão em  (LIMA, 1995).
(LIMA, 1995). .
. é limitado e
é limitado e 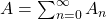 com
com 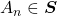 , para todo
, para todo 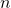 , então,
, então, 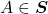 .
.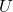 , para superfície unitária. Para quadrado unitário é, em geral, escolhido aquele cujo lado é um segmento unitário, isto é, de comprimento 1. Portanto, sejam
, para superfície unitária. Para quadrado unitário é, em geral, escolhido aquele cujo lado é um segmento unitário, isto é, de comprimento 1. Portanto, sejam 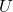 esse quadrado e
esse quadrado e 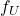 a função área tal que
a função área tal que 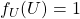 . Estabelece-se, então, a terminologia:
. Estabelece-se, então, a terminologia: 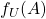 , é a Medida de Área da superfície
, é a Medida de Área da superfície  , na unidade de medida
, na unidade de medida 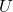 . Com isso, uma figura
. Com isso, uma figura  que se possa construir como união finita de quadrados unitários quase disjuntos pertence a
que se possa construir como união finita de quadrados unitários quase disjuntos pertence a  e o valor
e o valor 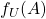 é o número de quadrados unitários contidos na figura (LIMA, 1995).
é o número de quadrados unitários contidos na figura (LIMA, 1995).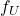 , os autores ressaltaram um instrumento fundamental que são as fórmulas de área. Se
, os autores ressaltaram um instrumento fundamental que são as fórmulas de área. Se  é um quadrado qualquer cujo lado tem comprimento de medida inteira
é um quadrado qualquer cujo lado tem comprimento de medida inteira  , pode-se ver, de imediato, que
, pode-se ver, de imediato, que 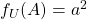 . Por subdivisão apropriada do lado do quadrado
. Por subdivisão apropriada do lado do quadrado 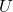 , deduz-se que, se
, deduz-se que, se  tem lado racional
tem lado racional  , também será
, também será 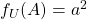 . Esta mesma fórmula vale mesmo se
. Esta mesma fórmula vale mesmo se  é irracional. Para se deduzir tal fato, no entanto, é necessário que se adote mais uma propriedade a ser verificada pela função
é irracional. Para se deduzir tal fato, no entanto, é necessário que se adote mais uma propriedade a ser verificada pela função 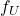 . A função
. A função 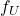 que o satisfaça poderá ser calculada em quadrados de lado com medida irracional e, mais geralmente ainda, em superfícies de fronteiras curvas. Uma formulação possível é:
que o satisfaça poderá ser calculada em quadrados de lado com medida irracional e, mais geralmente ainda, em superfícies de fronteiras curvas. Uma formulação possível é: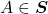 e
e 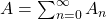 com
com 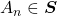 e
e 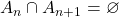 , então,
, então, 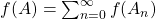 . (Expressão da Área como a soma de uma série).
. (Expressão da Área como a soma de uma série).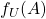 envolve a passagem ao limite de uma sequência de valores que são as somas parciais da série
envolve a passagem ao limite de uma sequência de valores que são as somas parciais da série 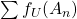 , onde
, onde 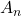 é uma das figuras que compõem
é uma das figuras que compõem  . Dessa forma surge o conceito de Área aproximada de uma superfície. O valor
. Dessa forma surge o conceito de Área aproximada de uma superfície. O valor 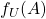 é, na prática, obtido pelo valor de somas parciais de
é, na prática, obtido pelo valor de somas parciais de 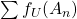 com a aproximação desejada (LIMA, 1995).
com a aproximação desejada (LIMA, 1995).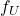 satisfazendo às condições acima referidas está definida em todos os quadrados, triângulos e em todas as superfícies que se decompõem em uniões finitas de triângulos cujos interiores sejam disjuntos dois a dois. Em suma, em toda superfície poligonal. Mais ainda, uma figura plana
satisfazendo às condições acima referidas está definida em todos os quadrados, triângulos e em todas as superfícies que se decompõem em uniões finitas de triângulos cujos interiores sejam disjuntos dois a dois. Em suma, em toda superfície poligonal. Mais ainda, uma figura plana  , mesmo não poligonal, isto é, com fronteiras curvas, que pode ser definida como união enumerável de superfícies mensuráveis, é mensurável (LIMA, 1995).
, mesmo não poligonal, isto é, com fronteiras curvas, que pode ser definida como união enumerável de superfícies mensuráveis, é mensurável (LIMA, 1995).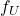 , definida em
, definida em  da forma indicada acima é única. Para isso, os autores consideraram, então,
da forma indicada acima é única. Para isso, os autores consideraram, então,  uma função área, definida em
uma função área, definida em  (satisfazendo, então, aos axiomas de positividade, aditividade e invariância por isometrias) tal que
(satisfazendo, então, aos axiomas de positividade, aditividade e invariância por isometrias) tal que 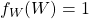 . A superfície
. A superfície 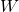 é uma nova superfície unitária. Seja
é uma nova superfície unitária. Seja 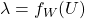 e tome a função
e tome a função 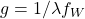 . Vemos que
. Vemos que 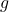 é também uma função área definida em
é também uma função área definida em  . Temos, portanto,
. Temos, portanto, 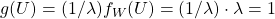 . Mas sabemos que a única função área que atende a essas condições é
. Mas sabemos que a única função área que atende a essas condições é 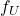 . Logo,
. Logo, 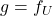 , isto é,
, isto é, 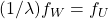 e, portanto,
e, portanto, 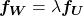 . Isto é, dadas duas funções área quaisquer,
. Isto é, dadas duas funções área quaisquer, 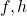 , definidas em
, definidas em  , elas diferem apenas por um fator de proporcionalidade. A questão que o autor põe neste ponto é a de explicitar uma estrutura matemática na qual se defina o termo área.
, elas diferem apenas por um fator de proporcionalidade. A questão que o autor põe neste ponto é a de explicitar uma estrutura matemática na qual se defina o termo área. , definida em
, definida em  , verificamos sua sobrejeção, isto é, dado um valor real positivo
, verificamos sua sobrejeção, isto é, dado um valor real positivo 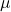 , existe uma superfície
, existe uma superfície  , tal que
, tal que 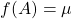 . Mas
. Mas  não é injetiva, pois há um conjunto de superfícies de
não é injetiva, pois há um conjunto de superfícies de  , representado por
, representado por 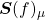 , tal que, para toda superfície
, tal que, para toda superfície  em
em 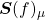 , tem-se
, tem-se 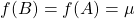 (LIMA, 1995).
(LIMA, 1995). pode ser dividido em classes disjuntas. Além disso, essas classes de equivalência não dependem da função área escolhida. Em outras palavras, partir de outra função área,
pode ser dividido em classes disjuntas. Além disso, essas classes de equivalência não dependem da função área escolhida. Em outras palavras, partir de outra função área, 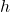 , (que se sabe, é igual a
, (que se sabe, é igual a 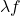 , para algum
, para algum 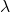 ), podemos ver que
), podemos ver que 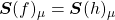 , para todo
, para todo 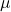 . Concluímos que
. Concluímos que  fica dividido em classes disjuntas
fica dividido em classes disjuntas 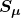 . O conjunto dessas classes,
. O conjunto dessas classes, 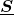 , é o conjunto das áreas. Dada uma superfície
, é o conjunto das áreas. Dada uma superfície  , sua classe,
, sua classe, 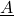 , é a Área
, é a Área 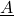 , isto é, o conjunto de todas as superfícies que têm a mesma Área que
, isto é, o conjunto de todas as superfícies que têm a mesma Área que  , quando medidas por qualquer função área (LIMA, 1995).
, quando medidas por qualquer função área (LIMA, 1995).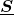 constituído, os autores puderam definir uma relação de ordem e duas operações, a adição de duas classes e a multiplicação de uma classe por um número, que satisfazem a propriedades análogas às de um espaço vetorial unidimensional sobre os reais. O conjunto
constituído, os autores puderam definir uma relação de ordem e duas operações, a adição de duas classes e a multiplicação de uma classe por um número, que satisfazem a propriedades análogas às de um espaço vetorial unidimensional sobre os reais. O conjunto 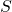 é uma estrutura matemática que permite o tratamento abstrato do conceito de Área, sendo um caso particular de um “domínio de quantidades”.
é uma estrutura matemática que permite o tratamento abstrato do conceito de Área, sendo um caso particular de um “domínio de quantidades”. uma função definida em
uma função definida em ![Rendered by QuickLaTeX.com [a, b]](https://blogs.multimeios.ufc.br/fernandacarmo/wp-content/ql-cache/quicklatex.com-b28ebca9266518f1a778b4a4b102a2e1_l3.png) e
e 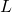 um número real. Dizemos que
um número real. Dizemos que 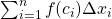 tende a
tende a 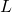 , quando
, quando 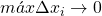 , e escrevemos
, e escrevemos 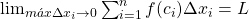 se, para todo
se, para todo 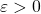 , existir um
, existir um 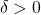 que só dependa de
que só dependa de  mas não da particular escolha dos
mas não da particular escolha dos 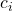 , tal que
, tal que 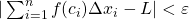 para toda partição
para toda partição 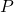 de
de ![Rendered by QuickLaTeX.com [a, b]](https://blogs.multimeios.ufc.br/fernandacarmo/wp-content/ql-cache/quicklatex.com-b28ebca9266518f1a778b4a4b102a2e1_l3.png) , com
, com 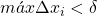 .
.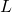 , que quando existe é único, denomina-se integral de Riemann de
, que quando existe é único, denomina-se integral de Riemann de  em
em ![Rendered by QuickLaTeX.com [a, b]](https://blogs.multimeios.ufc.br/fernandacarmo/wp-content/ql-cache/quicklatex.com-b28ebca9266518f1a778b4a4b102a2e1_l3.png) e indica-se por
e indica-se por 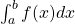 . Então, por definição
. Então, por definição 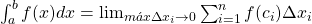 .
.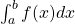 existe, então diremos que
existe, então diremos que  é integrável segundo Riemann em
é integrável segundo Riemann em ![Rendered by QuickLaTeX.com [a, b]](https://blogs.multimeios.ufc.br/fernandacarmo/wp-content/ql-cache/quicklatex.com-b28ebca9266518f1a778b4a4b102a2e1_l3.png) .
.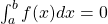 e
e 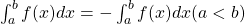 .
.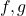 integráveis em
integráveis em ![Rendered by QuickLaTeX.com [a, b]](https://blogs.multimeios.ufc.br/fernandacarmo/wp-content/ql-cache/quicklatex.com-b28ebca9266518f1a778b4a4b102a2e1_l3.png) e
e 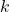 uma constante. Então,
uma constante. Então,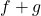 é integrável em
é integrável em ![Rendered by QuickLaTeX.com [a, b]](https://blogs.multimeios.ufc.br/fernandacarmo/wp-content/ql-cache/quicklatex.com-b28ebca9266518f1a778b4a4b102a2e1_l3.png) e
e![Rendered by QuickLaTeX.com \int_{a}^{b}[f(x)+g(x)]dx=\int_{a}^{b}f(x)dx+ \int_{a}^{b}g(x)dx](https://blogs.multimeios.ufc.br/fernandacarmo/wp-content/ql-cache/quicklatex.com-6e260d20f5a8ba7a0b946c954ddbf0e1_l3.png) .
.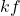 é integrável em
é integrável em ![Rendered by QuickLaTeX.com [a, b]](https://blogs.multimeios.ufc.br/fernandacarmo/wp-content/ql-cache/quicklatex.com-b28ebca9266518f1a778b4a4b102a2e1_l3.png) e
e 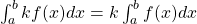 .
.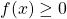 em
em ![Rendered by QuickLaTeX.com [a, b]](https://blogs.multimeios.ufc.br/fernandacarmo/wp-content/ql-cache/quicklatex.com-b28ebca9266518f1a778b4a4b102a2e1_l3.png) , então
, então 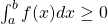 .
.![Rendered by QuickLaTeX.com c \in \; ]a, b[](https://blogs.multimeios.ufc.br/fernandacarmo/wp-content/ql-cache/quicklatex.com-730fbed4fd42c6b90340168430b182ce_l3.png) e
e  é integrável em
é integrável em ![Rendered by QuickLaTeX.com [a, c]](https://blogs.multimeios.ufc.br/fernandacarmo/wp-content/ql-cache/quicklatex.com-232b87f588bd0f107432d1283d8d6007_l3.png) e em
e em ![Rendered by QuickLaTeX.com [c, b]](https://blogs.multimeios.ufc.br/fernandacarmo/wp-content/ql-cache/quicklatex.com-41025a54faddc768ddcc34d10fbe66aa_l3.png) então
então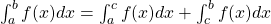 .
. contínua em
contínua em ![Rendered by QuickLaTeX.com [a, b]](https://blogs.multimeios.ufc.br/fernandacarmo/wp-content/ql-cache/quicklatex.com-b28ebca9266518f1a778b4a4b102a2e1_l3.png) , com
, com 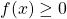 em
em ![Rendered by QuickLaTeX.com [a, b]](https://blogs.multimeios.ufc.br/fernandacarmo/wp-content/ql-cache/quicklatex.com-b28ebca9266518f1a778b4a4b102a2e1_l3.png) . Podemos definir a Área do conjunto
. Podemos definir a Área do conjunto  do plano limitado pelas retas
do plano limitado pelas retas  ,
, 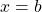 ,
, 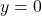 e pelo gráfico de
e pelo gráfico de 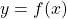 .
.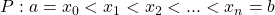 uma partição de
uma partição de ![Rendered by QuickLaTeX.com [a, b]](https://blogs.multimeios.ufc.br/fernandacarmo/wp-content/ql-cache/quicklatex.com-b28ebca9266518f1a778b4a4b102a2e1_l3.png) e sejam
e sejam 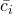 e
e 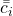 em
em ![Rendered by QuickLaTeX.com [x_{i-1}, x_{i}]](https://blogs.multimeios.ufc.br/fernandacarmo/wp-content/ql-cache/quicklatex.com-a0eeadd798a1ae81be66ce94f3679ca1_l3.png) tais que
tais que 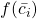 é o valor mínimo e
é o valor mínimo e 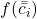 o valor máximo de
o valor máximo de  em
em ![Rendered by QuickLaTeX.com [x_{i-1}, x_{i}]](https://blogs.multimeios.ufc.br/fernandacarmo/wp-content/ql-cache/quicklatex.com-a0eeadd798a1ae81be66ce94f3679ca1_l3.png) . Uma definição para a Área de
. Uma definição para a Área de  deverá implicar que a soma de Riemann
deverá implicar que a soma de Riemann 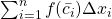 seja uma aproximação por falta da Área de
seja uma aproximação por falta da Área de  e que
e que 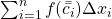 seja uma aproximação por excesso, isto é,
seja uma aproximação por excesso, isto é, 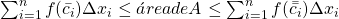 .
.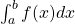 , quando
, quando 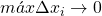 , nada mais natural do que definir a Área de
, nada mais natural do que definir a Área de  por
por 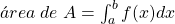 .
. no caso em que
no caso em que  é uma função integrável qualquer, com
é uma função integrável qualquer, com 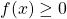 em
em ![Rendered by QuickLaTeX.com [a, b]](https://blogs.multimeios.ufc.br/fernandacarmo/wp-content/ql-cache/quicklatex.com-b28ebca9266518f1a778b4a4b102a2e1_l3.png) .
.![Rendered by QuickLaTeX.com \pi \int_{a}^{b} [f(x)]^{2} dx](https://blogs.multimeios.ufc.br/fernandacarmo/wp-content/ql-cache/quicklatex.com-47d59ce87fefac0352e15a90d870d70b_l3.png) é a fórmula que fornece o Volume do sólido de revolução obtido pela rotação, em torno do eixo
é a fórmula que fornece o Volume do sólido de revolução obtido pela rotação, em torno do eixo  , do conjunto
, do conjunto 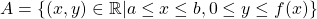 . Observemos que
. Observemos que ![Rendered by QuickLaTeX.com A(x)= \pi [f(x)]^{2}](https://blogs.multimeios.ufc.br/fernandacarmo/wp-content/ql-cache/quicklatex.com-1b163a2cfa63619bd76f2efd16e6a09e_l3.png) é a Área de interseção do sólido com o plano perpendicular ao eixo
é a Área de interseção do sólido com o plano perpendicular ao eixo  e passando pelo ponto de abcissa
e passando pelo ponto de abcissa  . Assim, o Volume mencionado anteriormente pode ser colocado na forma
. Assim, o Volume mencionado anteriormente pode ser colocado na forma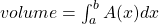 .
. um sólido qualquer, não necessariamente de revolução e seja
um sólido qualquer, não necessariamente de revolução e seja  um eixo escolhido arbitrariamente. Suponhamos que o sólido esteja compreendido entre dois planos perpendiculares a
um eixo escolhido arbitrariamente. Suponhamos que o sólido esteja compreendido entre dois planos perpendiculares a  , que interceptam o eixo
, que interceptam o eixo  em
em  e em
e em 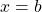 . Seja
. Seja 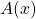 a Área de interseção do sólido com o plano perpendicular a
a Área de interseção do sólido com o plano perpendicular a  no ponto de abscissa
no ponto de abscissa  . Suponhamos que a função
. Suponhamos que a função 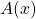 seja integrável em
seja integrável em ![Rendered by QuickLaTeX.com [a, b]](https://blogs.multimeios.ufc.br/fernandacarmo/wp-content/ql-cache/quicklatex.com-b28ebca9266518f1a778b4a4b102a2e1_l3.png) . Definimos, então, o Volume do sólido por
. Definimos, então, o Volume do sólido por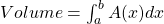 .
.